Question

已知中心在原点O，焦点在x轴上，离心率为的椭圆过点(，)．

(Ⅰ) 求椭圆的方程；

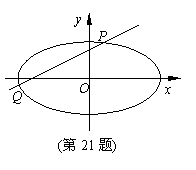
(Ⅱ) 设不过原点O的直线l与该椭圆交于P，Q两点，满足直线OP，PQ，OQ的斜率依次成等比数列，求△OPQ面积的取值范围．

 

Answer 1

本题主要考查椭圆的标准方程的求解，直线与椭圆的位置关系等基础知识，同时考查解析几何的基本思想方法和综合解题能力。满分15分。

(Ⅰ) 解：由题意可设椭圆方程为  (a＞b＞0)，

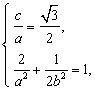则    故

所以，椭圆方程为 ．     ……………………………5分

(Ⅱ) 解：由题意可知，直线l的斜率存在且不为0，

故可设直线l的方程为 y＝kx＋m (m≠0)，P(x₁，y₁)，Q(x₂，y₂)，

由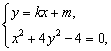 消去y得

(1＋4k²)x²＋8kmx＋4(m²－1)＝0，

则Δ＝64 k²b²－16(1＋4k²b²)(b²－1)＝16(4k²－m²＋1)＞0，

且，．

故 y₁ y₂＝(kx₁＋m)(kx₂＋m)＝k²x₁x₂＋km(x₁＋x₂)＋m²．……………………8分

因为直线OP，PQ，OQ的斜率依次成等比数列，

所以 ＝＝k²，

即 ＋m²＝0，又m≠0，

所以 k²＝，即 k＝……………………11分

由于直线OP，OQ的斜率存在，且Δ＞0，得

0＜m²＜2 且 m²≠1．

设d为点O到直线l的距离，

则 S_△OPQ＝d | PQ |＝| x₁－x₂ | | m |＝，

所以 S_△OPQ的取值范围为 (0，1)．     ……………………………15分