Question

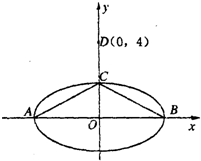已知椭圆G的方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，它与x轴交于A、B两点，与y轴正半轴交于C点，点D（0，4），若

AC

•

BC

=-3，|

BD

|=2

5

．
（I）求椭圆G的方程；
（II）过点D的直线l交椭圆G于M，N两点，若∠NMO=90°，求|MN|的长．

Answer 1

分析：（I）由题意，A（-a，0），B（a，0），C（0，b），D（0，4），利用

AC

•

BC

=-3，|

BD

|=2

5

，建立方程组，即可求得椭圆G的方程；
（II）设M（x₁，y₁），N（x₂，y₂），根据∠NMO=90°，求得直线l的斜率，从而假设直线l的方程与椭圆G联立，再利用弦长公式即可得到结论．

解答：解：（I）由题意，A（-a，0），B（a，0），C（0，b），D（0，4）
∵

AC

•

BC

=-3，|

BD

|=2

5

∴

(a，b)•(-a，b)=-3 a2+42 =2 5

∴a²=4，b²=1
∴椭圆G的方程为

x2

4

+y2=1；
（II）设M（x₁，y₁），N（x₂，y₂），∴

x12+4y12=4 y1-4 x1 × y1 x1 =-1

，解得x1=±

2 5

3

， y1=

2

3

∴直线l的斜率为k=±

5

设直线l的方程为y=±

5

x+4，与椭圆G联立

y=± 5 x+4 x2 4 +y2=1

，消元可得21x2±32

5

x+60=0
解得x1+x2=±

32 5

21

，x1x2=

60

21

∴|MN|=

1+k2

×

(x1+x2)2-4x1x2

=

1+5

×

(± 32 5 21 )2-4× 60 21

=

4 30

21

点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查弦长公式，解题的关键是直线与椭圆方程联立，利用韦达定理解题．