题目内容
已知函数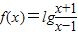
．（Ⅰ）求f（x）的值域；
（Ⅱ）讨论f（x）的奇偶性．
【答案】分析：（Ⅰ）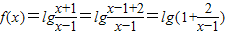
，由
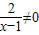，对数函数的性质即可求得函数f（x）的值域；
（Ⅱ）先求得函数定义域，看是否关于原点对称，再研究f（-x）与f（x）的关系，根据函数奇偶性的定义即可得到结论．
解答：解：（Ⅰ）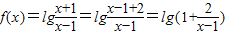
，
∵
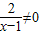，∴f（x）≠lg1，即f（x）≠0．
∴函数f（x）的值域为（-∞，0）∪（0，+∞）．
（Ⅱ）由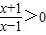
得x＜-1，或x＞1．
∴函数f（x）的定义域为{x|x＜-1，或x＞1}，它关于原点对称．
∵
，
，
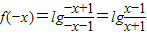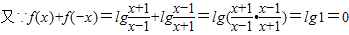∴f（-x）=-f（x）．
故函数f（x）是奇函数．
点评：本题考查函数奇偶性的判断及函数值域的求解，属中档题，定义是解决该类问题的基本方法．
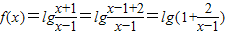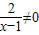，由，对数函数的性质即可求得函数f（x）的值域；（Ⅱ）先求得函数定义域，看是否关于原点对称，再研究f（-x）与f（x）的关系，根据函数奇偶性的定义即可得到结论．
解答：解：（Ⅰ）
，∵
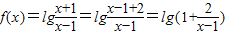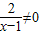，∴f（x）≠lg1，即f（x）≠0．∴函数f（x）的值域为（-∞，0）∪（0，+∞）．
（Ⅱ）由
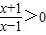得x＜-1，或x＞1．∴函数f（x）的定义域为{x|x＜-1，或x＞1}，它关于原点对称．
∵
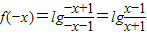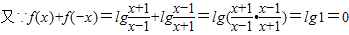，，∴f（-x）=-f（x）．
故函数f（x）是奇函数．
点评：本题考查函数奇偶性的判断及函数值域的求解，属中档题，定义是解决该类问题的基本方法．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
．
．
个单位，得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．
．
上恒成立，求实数m的取值范围．
．
成等差数列，且
=9，求a的值．
．