题目内容
设 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足;
满足;
(i) ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 .
.
那么称这两个集合“保序同构”.现给出以下3对集合:
① ;
;
② ;
;
③ .
.
其中,“保序同构”的集合对的序号是____________(写出所有“保序同构”的集合对的序号)
①②③
解析试题分析:根据题意,设 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足条件
满足条件 ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 时,则两个集合为“保序同构”,
时,则两个集合为“保序同构”,
即定义域对应的函数为增函数,那么对于① ;则可知满足题意。
;则可知满足题意。
② ;可知成立
;可知成立
③ .比如y=x,满足题意。故答案为①②③
.比如y=x,满足题意。故答案为①②③
考点:集合的运算
点评:主要是考查了集合的新定义的运用,属于基础题。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,A
,A ,B
,B ,那么
,那么 __.
__. ,
, ,则
,则 .
.  的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 ,若
,若 ,
, ,则实数
,则实数 的取值范围是
的取值范围是  ,
, ,如果
,如果 ,则
,则 .
. ,如果
,如果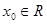 满足:对任意
满足:对任意 ,都存在
,都存在 ,使得
,使得 ,那么称
,那么称 为集合
为集合 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1) ;(2)
;(2) ;(3)
;(3) ;(4)
;(4) ,以
,以 为聚点的集合有
为聚点的集合有  则
则 就称
就称 是“和谐”集合。则在集合
是“和谐”集合。则在集合 的所有非空子集中,“和谐”集合的概率是 .
的所有非空子集中,“和谐”集合的概率是 . ,集合
,集合 , 则
, 则 __________.
__________.  ,则
,则 = .
= .