题目内容
已知函数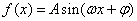
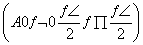一个周期的图像如图所示．
(1)求函数f(x)的表达.
(2)若f(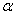
)＋
＝
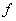
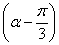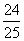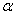，且为△ABC的一个内角，求sinα＋cosα.
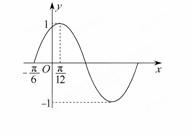
解:(1)由图知，函数的最大值为1，则A＝1，
∴函数f(x)的表达式为f(x)＝sin
化简，得sin2α＝.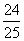
∴(sinα＋cosα)2＝1＋sin2α＝
.
由于0＜α＜π，则0＜2α＜2π，
但sin2α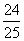＝＞0，则0＜2α＜π，即α为锐角，
从而sinα＋cosα＞0，因此sinα＋cosα＝
.
练习册系列答案
相关题目
满足条件
，则
的值为（ ）
的值有关
中，内角
所对的边分别为
，给出下列结论：
，则
；
，则
成立；
，则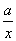
在区间[1,2]上都是减函数,则a的取值范围是 ( )
，tanβ＝
，且α、β∈
.
.
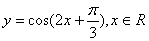的图象，只需把函数
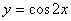的图象 （ ）
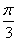个单位长度 B. 向右平行移动
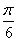个单位长度 D. 向右平行移动
中,M是BC的中点，AM=1,点P在AM上且满足
,则
等于 （ ）
B. 
C. 
D. 
的概率 
B. 
C. 
D. 
直线l1：（
﹣1）x+y﹣2=0与直线l2：（+1）x﹣y﹣3=0的位置关系是（ ）
|
| A． | 平行 | B． | 相交 | C． | 垂直 | D． | 重合 |