题目内容

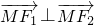椭圆 $数学公式$ 的左、右焦点分别是F₁、F₂，若点M在椭圆上，且满足 $数学公式$ ，则△MF₁F₂面积为________．

9
分析：令|F₁P|=m、|PF₂|=n，由椭圆的定义可得 m+n=2a①，Rt△F₁PF₂中，由勾股定理可得m²+n²②，由①②可得m•n的值，利用△F₁PF₂的面积是 $\text{[math]}$ m•n求得结果．
解答：由椭圆的方程可得 a=5，b=3，c=4，令|F₁P|=m、|PF₂|=n，
由椭圆的定义可得 m+n=2a=10 ①，Rt△F₁PF₂ 中，
由勾股定理可得（2c）²=m²+n²，m²+n²=64②，
由①②可得m•n=18，
∴△F₁PF₂的面积是 $\text{[math]}$ m•n=9，
故答案为：9．
点评：本题考查椭圆的简单性质和定义，以及勾股定理的应用，属于基础题．．

练习册系列答案

中考升学指导系列答案

超越中考系列答案

中考全程复习训练系列答案

京版教材配套资源英语新视野系列答案

自主学语文系列答案

每日10分钟口算心算速算天天练系列答案

每时每刻快乐优加系列答案

孟建平培优一号系列答案

孟建平毕业总复习系列答案

密解1对1系列答案

相关题目

=1（a＞b＞0）的离心率为

，以原点为圆心，椭圆短半轴长为半径的圆与y=x+2相切．
（1）求a与b；
（2）设该椭圆的左、右焦点分别为F₁和F₂，直线l过F₂且与x轴垂直，动直线l₂与y轴垂直，l₂交l₁与点P．求PF₁线段垂直平分线与l₂的交点M的轨迹方程，并说明曲线类型．

给出以下5个命题：
①曲线x²-（y-1）²=1按

=(1，-2)平移可得曲线（x+1）²-（y-3）²=1；
②设A、B为两个定点，n为常数，|

|=n，则动点P的轨迹为双曲线；
③若椭圆的左、右焦点分别为F₁、F₂，P是该椭圆上的任意一点，延长F₁P到点M，使|F₂P|=|PM|，则点M的轨迹是圆；
④A、B是平面内两定点，平面内一动点P满足向量

夹角为锐角θ，且满足 |

=0，则点P的轨迹是圆（除去与直线AB的交点）；
⑤已知正四面体A-BCD，动点P在△ABC内，且点P到平面BCD的距离与点P到点A的距离相等，则动点P的轨迹为椭圆的一部分．
其中所有真命题的序号为

已知椭圆的左、右焦点分别为F₁，F₂，椭圆的离心率为

且经过点P(1，

)．M为椭圆上的动点，以M为圆心，MF₂为半径作圆M．
（1）求椭圆C的标准方程；
（2）若圆M与y轴有两个交点，求点M横坐标的取值范围；
（3）是否存在定圆N，使得圆N与圆M相切？若存在．求出圆N的方程；若不存在，说明理由．

（2011•重庆一模）给出以下4个命题：
①曲线x²-（y-1）²=1按

=（1，-2）平移可得曲线（x+1）²-（y-3）²=1；
②若|x-1|+|y-1|≤1，则使x-y取得最小值的最优解有无数多个；
③设A、B为两个定点，n为常数，|

|=n，则动点P的轨迹为双曲线；
④若椭圆的左、右焦点分别为F₁、F₂，P是该椭圆上的任意一点，延长F₁P到点M，使|F₂P|=|PM|，则点M的轨迹是圆．
其中所有真命题的序号为

（本题12分）已知椭圆的左、右焦点分别为F₁、F₂，其中F₂也是抛物线的焦点，M是C₁与C₂在第一象限的交点，且

（I）求椭圆C₁的方程；（II）已知菱形ABCD的顶点A、C在椭圆C₁上，顶点B、D在直线上，求直线AC的方程。