ЬтФПФкШн
ЁОЬтФПЁП2018ФъЃЌНЬг§ВПЗЂЮФШЗЖЈаТИпПМИФИяе§ЪНЦєЖЏЃЌКўФЯЁЂЙуЖЋЁЂКўББЕШ8ЪЁЪаПЊЪМЪЕаааТИпПМжЦЖШЃЌДг2018ФъЯТбЇЦкЕФИпвЛФъМЖбЇЩњПЊЪМЪЕаа.ЮЊСЫЪЪгІаТИпПМИФИяЃЌФГаЃзщжЏСЫвЛДЮаТИпПМжЪСПВтЦРЃЌдкГЩМЈЭГМЦЗжЮіжаЃЌИпЖўФГАрЕФЪ§бЇГЩМЈЕФОЅвЖЭМКЭЦЕТЪЗжВМжБЗНЭМвђЙЪЖМЪмЕНВЛЭЌГЬЖШЕФЫ№ЛЕЃЌЕЋПЩМћВПЗжШчЯТЃЌОнДЫНтД№ШчЯТЮЪЬтЃК
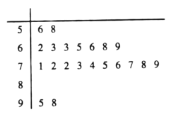
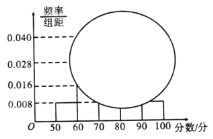
ЃЈ1ЃЉЧѓИУАрЪ§бЇГЩМЈдк![]() ЕФЦЕТЪМАШЋАрШЫЪ§ЃЛ
ЕФЦЕТЪМАШЋАрШЫЪ§ЃЛ
ЃЈ2ЃЉИљОнЦЕТЪЗжВМжБЗНЭМЙРМЦИУАретДЮВтЦРЕФЪ§бЇЦНОљЗжЃЛ
ЃЈ3ЃЉШєЙцЖЈ![]() ЗжМАЦфвдЩЯЮЊгХауЃЌЯжДгИУАрЗжЪ§дк
ЗжМАЦфвдЩЯЮЊгХауЃЌЯжДгИУАрЗжЪ§дк![]() ЗжМАЦфвдЩЯЕФЪдОэжаШЮШЁ
ЗжМАЦфвдЩЯЕФЪдОэжаШЮШЁ![]() ЗнЗжЮібЇЩњЕУЗжЧщПіЃЌЧѓдкГщШЁЕФ
ЗнЗжЮібЇЩњЕУЗжЧщПіЃЌЧѓдкГщШЁЕФ![]() ЗнЪдОэжажСЩйга
ЗнЪдОэжажСЩйга![]() ЗнгХауЕФИХТЪ.
ЗнгХауЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉЦЕТЪЮЊ![]() ЃЌШЋАрШЫЪ§ЮЊ
ЃЌШЋАрШЫЪ§ЮЊ![]() .ЃЈ2ЃЉ73.8ЃЛЃЈ3ЃЉ
.ЃЈ2ЃЉ73.8ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМаЁОиаЮЕФУцЛ§МДЮЊЦЕТЪЃЌЦЕЪ§![]() ЦЕТЪМДЕУГіШЋАрШЫЪ§.
ЦЕТЪМДЕУГіШЋАрШЫЪ§.
ЃЈ2ЃЉИљОнЦЕТЪЗжВМЭМЦНОљЪ§![]() УПИіаЁОиаЮЕзБпжаЕуКсзјБъ
УПИіаЁОиаЮЕзБпжаЕуКсзјБъ![]() аЁОиаЮЕФУцЛ§ЃЌДњШыЪ§ОнМДПЩЧѓНт.
аЁОиаЮЕФУцЛ§ЃЌДњШыЪ§ОнМДПЩЧѓНт.
ЃЈ3ЃЉСаГіЛљБОЪТМўЃЌИљОнЙХЕфИХаЭЕФИХТЪЧѓЗЈМДПЩЧѓНт.
ЃЈ1ЃЉЦЕТЪЮЊ![]() ЃЌЦЕЪ§=2ЃЌЫљвдШЋАрШЫЪ§ЮЊ
ЃЌЦЕЪ§=2ЃЌЫљвдШЋАрШЫЪ§ЮЊ![]()
![]() .
.
ЃЈ2ЃЉЙРМЦЦНОљЗжЮЊЃК![]()
![]() .
.
ЃЈ3ЃЉгЩвбжЊЕУ![]() ЕФШЫЪ§ЮЊЃКЃЈ0.16+0.08ЃЉ
ЕФШЫЪ§ЮЊЃКЃЈ0.16+0.08ЃЉ![]()
![]() .
.
ЩшЗжЪ§дк![]() ЕФЪдОэЮЊ
ЕФЪдОэЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЗжЪ§дк
ЃЌЗжЪ§дк![]() ЕФЪдОэЮЊ
ЕФЪдОэЮЊ![]() ЃЌ
ЃЌ![]() .
.
дђДг![]() ЗнОэжаШЮШЁ
ЗнОэжаШЮШЁ![]() ЗнЃЌЙВга
ЗнЃЌЙВга![]() ИіЛљБОЪТМўЃЌ
ИіЛљБОЪТМўЃЌ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЦфжажСЩйгавЛЗнгХауЕФЪТМўЙВга![]() ИіЃЌ
ИіЃЌ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() дкГщШЁЕФ
дкГщШЁЕФ![]() ЗнЪдОэжажСЩйга
ЗнЪдОэжажСЩйга![]() ЗнгХауЕФИХТЪЮЊ
ЗнгХауЕФИХТЪЮЊ![]() .
.