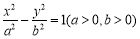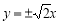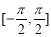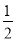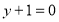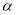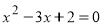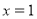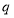题目内容
如图,在四棱锥 中,底面
中,底面 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且 交
交 于点
于点 .
.

(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
证明过程详见试题解析.
【解析】
试题分析:(Ⅰ)要证明
 平面
平面 ,就是要在平面
,就是要在平面 内找一条直线与直线
内找一条直线与直线 平行,显然
平行,显然 符合要求;(Ⅱ)要证明
符合要求;(Ⅱ)要证明 平面
平面 ,就是要在平面
,就是要在平面 内找两条相交直线与
内找两条相交直线与 垂直.显然
垂直.显然 符合要求.
符合要求.
试题解析:(Ⅰ)证明:在矩形 中,
中, , 又
, 又 平面
平面 ,
, 
 平面
平面 ,所以
,所以
 平面
平面 .
.
(Ⅱ)证明:如图在矩形 中,点
中,点 为
为 的中点, 又
的中点, 又 , 故
, 故 ,
, .又因为
.又因为 ,
, 
 平面
平面 , 所以
, 所以 平面
平面 .
.
考点:(Ⅰ)线面平行;(Ⅱ)线面垂直.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目