题目内容
若x＜3，则，f(x)=| 4 | x-3 |
分析：先将函数f(x)=
+x的解析式变为积为定值的形式，再有基本不等式求出最值
| 4 |
| x-3 |
解答：解：f(x)=
+x=
+x-3+3
由于x＜3，x-3＜0
故f(x)=
+x≤-2
+3=-1，当
=x-3，即x=1时等号成立
x＜3时，函数f(x)=
+x的最大值是-1
故答案为：-1．
| 4 |
| x-3 |
| 4 |
| x-3 |
由于x＜3，x-3＜0
故f(x)=
| 4 |
| x-3 |
|
| 4 |
| x-3 |
x＜3时，函数f(x)=
| 4 |
| x-3 |
故答案为：-1．
点评：本题考查基本不等式求最值，求解的关键是掌握住基本不等式求最值的规则，即积定和最小，和定积最大，在本题中构造出积为定值的形式，尤其重要，本题有一易错点，易忘记判断两个因子的符号，致使判断出的结果为大于等于7，做题时要注意避免此类失误．
练习册系列答案
相关题目
”表示两个正数间的一种运算：a
＋a＋b(a＞0，b＞0)
；
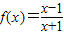，设f2（x）=f[f（x）]，f3（x）=f[f2（x）]，…，fn+1（x）=f[fn（x）]（n∈N*且n≥2），令集合M={x|f2009（x）=x，x∈R}，则集合M为空集．
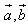的夹角为锐角”的充要条件是“
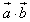＞0”；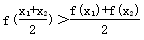
；