Question

在△ABC中，a，b，c分别为角A，B，C所对的边，且满足b=7asinB，则sinA=________，若B=60°，则sinC=________．

Answer 1

    
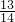
分析：根据正弦定理，得b=，与已知等式比较可得sinA=，而B=60°得sinB＞sinA，所以角A是锐角，由同角三角函数的平方关系算出cosA=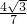，最后根据sinC=sin（A+B），结合两角和的正弦公式即可算出sinC的值．
解答：∵由正弦定理，得
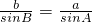
∴b==7asinB，解之得sinA=
∵B=60°，sinA=＜sinB=，得A为锐角
可得cosA=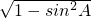=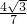（舍负）
∴sinC=sin（A+B）=sin（A+60°）=×+×=
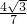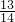
故答案为：，
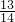
点评：本题给出三角形ABC中的边角关系式，求sinA和sinC的值，着重考查了运用正余弦定理解三角形和两角的正弦公式等知识，属于基础题．