Question

【题目】如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ ）离y轴最近的零点与最大值均在抛物线y=﹣ x2+ x+1上，则f（x）=（ ）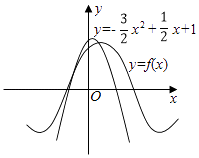

A.
B.

C.
D.

Answer 1

【答案】C
【解析】解：根据题意，函数f（x）离y轴最近的零点与最大值均在抛物线 上，
令y=0，得﹣ x2+ x+1=0，
解得x=﹣ 或x=1；
∴点（﹣ ，0）在函数f（x）的图像上，
∴﹣ ω+φ=0，即φ= ω①；
又令ωx+φ= ，得ωx= ﹣φ②；
把①代入②得，x= ﹣ ③；
令y=1，得﹣ x2+ x+1=1，
解得x=0或x= ；
即 ﹣ = ，
解得ω= π，
∴φ= ω= ，
∴f（x）=sin（ x+ ）．
故选：C．