题目内容
【题目】已知点Q是圆
上的动点，点
，若线段QN的垂直平分线MQ于点P.
(I)求动点P的轨迹E的方程
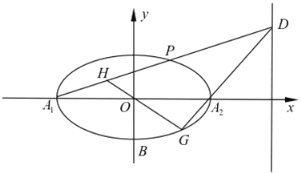
(II)若A是轨迹E的左顶点，过点D（-3，8）的直线l与轨迹E交于B，C两点，求证：直线AB、AC的斜率之和为定值.
【答案】(Ⅰ) 
(Ⅱ)见证明
【解析】
（Ⅰ）线段
的垂直平分线交
于点P，所以
，则
为定值，所以P的轨迹是以
为焦点的椭圆，结合题中数据求出椭圆方程即可；（Ⅱ）设出直线方程，联立椭圆方程得到韦达定理，写出
化简可得定值.
解：（Ⅰ）由题可知，线段的垂直平分线交于点P，
所以，则
，
所以P的轨迹是以为焦点的椭圆，
设该椭圆方程为
，
则
，所以
，
可得动点P的轨迹E的方程为.
（Ⅱ）由（Ⅰ）可得，过点D的直线
斜率存在且不为0，
故可设l的方程为
，
，
由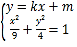
得
，
而
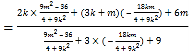
由于直线过点
，所以
，
所以
（即为定值）
练习册系列答案
相关题目
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
（1）求该单位员工当年年薪的平均值和中位数；
（2）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元，预测该员工第六年的年薪为多少？
附：线性回归方程
中系数计算公式分别为：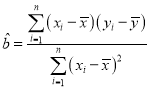
，
，其中
、
为样本均值.