题目内容
甲、乙、丙三人相互传球,球开始在甲手中,求经过5次传球后,球又回到甲手中的不同传球的方法数.经过n次传球呢?
分析：本题可通过画树枝图寻求解题思路.
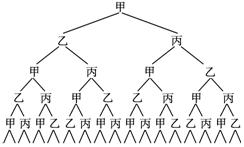
从上图发现经过n次传球共有2n种方法,第n-1次传球后不在甲手中的方法数与第n次传球后球在甲手中的方法数相同,为此可建立递推关系.
解：设经过n次传球后,球在甲手中的方法数为an.
依题意有an=2n-1-an-1.
令an+λ·2n=-(an-1+λ·2n-1),
则an=-an-1-3λ·2n-1,
∴λ=-
.
∴{an-
}是以-
为首项,公比为-1的等比数列.
∴an-
=-
·(-1)n-1.
∴an=
·2n-
(-1)n-1.
当n=5时,a5=10.
练习册系列答案
相关题目
甲、乙、丙、丁四人做相互传球练习，第一次甲传给其他三人中的一人，第二次由拿球者再传给其他三人中的一人，这样共传了4次，则第4次仍传回到甲的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
