Question

【题目】已知函数 的部分图象如图所示，f（x）的图象与x轴切于N点，则下列选项判断错误的是（ ）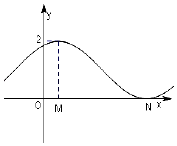

A.
B.
C.
D.|MN|=π

Answer 1

【答案】B
【解析】解：由函数 的部分图象知，

1+ω=2，解得ω=1，

∴f（x）=cos（x﹣ ）+1；

当x= 时，f（x）=2，为最大值，∴f（x）的图象关于直线x= 对称，

有f（ ﹣x）=f（ +x），∴A正确；

由于f（x）+f（ ﹣x）=cos（x﹣ ）+1+[cos（ ﹣x﹣ ）+1]

=2+cos（x﹣ ）+sinx

=2+ cosx+ sinx

=2+ sin（x+ ）≠2，∴B错误；

由于f（ ）=cos（ ﹣ ）+1=cos +1=1，∴C正确；

由于|MN|= T= ×2π=π，∴D正确．

所以答案是：B．