题目内容
1.已知平面内一动点M到两定点$B_1^{\;}({0,-1}),B_2^{\;}({0,1})$和连线的斜率之积为$-\frac{1}{2}$(1)求动点M的轨迹E的方程;
(2)设直线l:y=x+m与轨迹E交于A,B两点,线段AB的垂直平分线交x轴点P,当m变化时,求△PAB面积的最大值.
分析 (1)设出M的坐标,结合题意列式化简得答案;
(2)联立直线方程与椭圆方程,化为关于x的一元二次方程,利用弦长公式求得弦长,再由点到直线的距离公式求出P到AB的距离,代入三角形面积公式,然后利用基本不等式求最值.
解答 解:(1)设M的坐标为(x,y),
依题意得:$\frac{y+1}{x}•\frac{y-1}{x}=-\frac{1}{2}$,
化简得:$\frac{{x}^{2}}{2}+{y}^{2}=1(x≠0)$;
(2)设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=x+m}\end{array}\right.$,得3x2+4mx+2m2-2=0.
∵直线与椭圆有两个不同交点,
由根与系数的关系得:${x}_{1}+{x}_{2}=-\frac{4m}{3},{x}_{1}{x}_{2}=\frac{2{m}^{2}-2}{3}$.
∴△=(4m)2-12(2m2-2)>0,即$-\sqrt{3}<m<\sqrt{3}$且m≠-1,0,1.
设A,B中点为C,C点横坐标为${x}_{C}=\frac{{x}_{1}+{x}_{2}}{2}=-\frac{2m}{3}$,${y}_{C}={x}_{C}+m=\frac{m}{3}$.
∴$C(-\frac{2m}{3},\frac{m}{3})$,
∴线段AB的垂直平分线方程为$y-\frac{m}{3}=-(x+\frac{2m}{3})$,
∴P点坐标为($-\frac{m}{3},0$).
P到AB的距离d=$\frac{|\frac{2}{3}m|}{\sqrt{2}}$.
由弦长公式得:|AB|=$\sqrt{2}$•$\sqrt{({x}_{1}+x)^{2}-4{x}_{1}{x}_{2}}=\frac{\sqrt{2}}{3}•\sqrt{24-8{m}^{2}}$.
∴${S}_{△PAB}=\frac{1}{2}×\frac{|\frac{2}{3}m|}{\sqrt{2}}×\frac{\sqrt{2}}{3}=\frac{2\sqrt{2}}{9}\sqrt{{m}^{2}(3-{m}^{2})}$$≤\frac{2\sqrt{2}}{9}•\frac{{m}^{2}+3{-m}^{2}}{2}=\frac{\sqrt{2}}{3}$.
当且仅当${m}^{2}=\frac{3}{2}$,即m=$±\frac{\sqrt{6}}{2}$∈($-\sqrt{3},\sqrt{3}$)时等号成立.
∴△PAB面积的最大值为$\frac{\sqrt{2}}{3}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了弦长公式的应用,是中档题.

| A. | 0<a<$\frac{1}{3}$ | B. | 0<a<$\frac{2}{3}$ | C. | a>$\frac{2}{3}$ | D. | $\frac{2}{3}$<a<1 |
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
| A. | 有一个对称中心$({\frac{π}{12},0})$ | B. | 有一条对称轴$x=\frac{π}{6}$ | ||
| C. | 在区间$[{-\frac{π}{12},\frac{5π}{12}}]$上单调递减 | D. | 在区间$[{-\frac{5π}{12},\frac{π}{12}}]$上单调递增 |
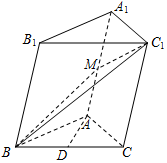 在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.
在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.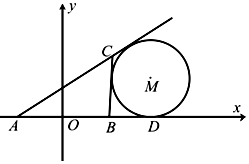 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.