题目内容
已知数列{an}满足: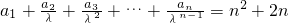 (其中常数λ>0,n∈N*).
(其中常数λ>0,n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:当λ=4时,数列{an}中的任何三项都不可能成等比数列;
(Ⅲ)设Sn为数列{an}的前n项和.求证:若任意n∈N*,(1-λ)Sn+λan≥3.
(Ⅰ)解:由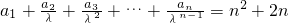 ①,
①,
取n=1时,求得a1=3,
当n≥2时,有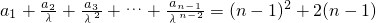 ②,
②,
①-②得: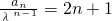 .∴
.∴ .
.
又a1=3也适合上式,
所以,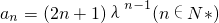 .
.
(Ⅱ)证明:当λ=4时,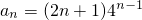 .
.
下面用反证法证明
假设存在ar,as,at成等比数列,
则[(2r+1)•4r-1]•[(2t+1)•4t-1]=(2s+1)2•42s-2.
整理得(2r+1)(2t+1)•4r+t-2s=(2s+1)2.
等式右边为奇数,要使左边等于右边,则r+t-2s=0.
所以,(2r+1)(2t+1)=(r+t+1)2,整理得(r-t)2=0,∴r=t.这与r≠t矛盾,
故不存在这样的正整数r,s,t,使得ar,as,at成等比数列.
(Ⅲ)证明:Sn=a1+a2+…+an
=3+5λ+7λ2+…+(2n+1)λn-1.
当λ=1时, .
.
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1③.
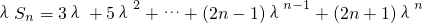 ④.
④.
③-④得: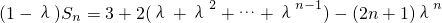
=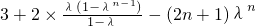 .
.
所以,当λ=1时,不等式左边=(1-λ)Sn+λan=an=2n+1≥3,结论显然成立;
当λ≠1时,不等式左边=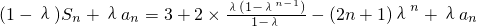
=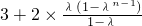 .
.
而λ>0,1-λ和1-λn-1同号,故 .
.
∴(1-λ)Sn+λan≥3.
综上,(1-λ)Sn+λan≥3对任意n∈N*都成立.
分析:(Ⅰ)由给出的递推式知,n=1时,a1=3,n≥2时,在递推式中取n=n-1得另一递推式,两式作差后可求an,验证首项后即可得到数列{an}的通项公式;
(Ⅱ)在数列{an}的通项公式中,把λ值代4,利用反证法证明不存在正整数r,s,t,使得ar,as,at成等比数列;
(Ⅲ)当λ=1时,利用等差数列求和求出Sn,当λ≠1时,利用错位相减法求出Sn,把求得的an和Sn代入要求证的不等式左边,整理后即可得到结论.
点评:本题考查了等比关系的确定,考查了利用错位相减法求数列的前n项和,考查了分类讨论得数学思想,训练了反证法,体现了整体代换思想,是很好的数列与不等式综合题.属中高档题.
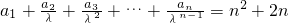 ①,
①,取n=1时,求得a1=3,
当n≥2时,有
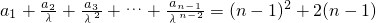 ②,
②,①-②得:
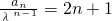 .∴
.∴ .
.又a1=3也适合上式,
所以,
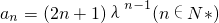 .
.(Ⅱ)证明:当λ=4时,
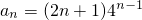 .
.下面用反证法证明
假设存在ar,as,at成等比数列,
则[(2r+1)•4r-1]•[(2t+1)•4t-1]=(2s+1)2•42s-2.
整理得(2r+1)(2t+1)•4r+t-2s=(2s+1)2.
等式右边为奇数,要使左边等于右边,则r+t-2s=0.
所以,(2r+1)(2t+1)=(r+t+1)2,整理得(r-t)2=0,∴r=t.这与r≠t矛盾,
故不存在这样的正整数r,s,t,使得ar,as,at成等比数列.
(Ⅲ)证明:Sn=a1+a2+…+an
=3+5λ+7λ2+…+(2n+1)λn-1.
当λ=1时,
 .
.当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1③.
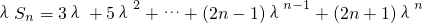 ④.
④.③-④得:
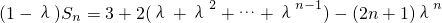
=
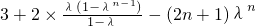 .
.所以,当λ=1时,不等式左边=(1-λ)Sn+λan=an=2n+1≥3,结论显然成立;
当λ≠1时,不等式左边=
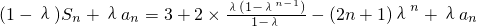
=
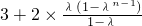 .
.而λ>0,1-λ和1-λn-1同号,故
 .
.∴(1-λ)Sn+λan≥3.
综上,(1-λ)Sn+λan≥3对任意n∈N*都成立.
分析:(Ⅰ)由给出的递推式知,n=1时,a1=3,n≥2时,在递推式中取n=n-1得另一递推式,两式作差后可求an,验证首项后即可得到数列{an}的通项公式;
(Ⅱ)在数列{an}的通项公式中,把λ值代4,利用反证法证明不存在正整数r,s,t,使得ar,as,at成等比数列;
(Ⅲ)当λ=1时,利用等差数列求和求出Sn,当λ≠1时,利用错位相减法求出Sn,把求得的an和Sn代入要求证的不等式左边,整理后即可得到结论.
点评:本题考查了等比关系的确定,考查了利用错位相减法求数列的前n项和,考查了分类讨论得数学思想,训练了反证法,体现了整体代换思想,是很好的数列与不等式综合题.属中高档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目