Question

如果要测量某铁塔PO的高度,但不能到达铁塔的底部,在只能使用简单的测量工具的前提下,你能设计出哪些测量方法?并提供每种方法的计算公式.

   

Answer 1

思路分析：要测量铁塔的高度,只能在铁塔底部所在的平面上选取两点,量出两点间的距离,再测量有关角,从而构造三角形求解.

    解:测量方法一:

    在地面上引一条基线AB,这条基线和塔底在同一水平面上,且延长后不过塔底,测出AB的长,用经纬仪测出角β、γ和A对塔顶P的仰角α的大小,则可求出铁塔PO的高.

    计算方法如下:

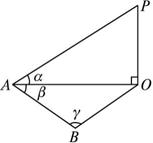
    如上图所示,在△ABO中,由正弦定理得

AO==,

    在Rt△PAO中,PO=AO·tanα,

∴PO=.

    测量方法二:

    在地面上引一条基线AB,这一基线与塔底在同一水平面上,并使A、B、O三点在一条直线上,测出AB的长和A、B对塔顶P的仰角α、β,则可求出铁塔PO的高.

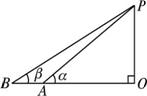
    计算方法如下:

    如图所示,在△PAB中,由正弦定理得PA=·sinβ=,

    在Rt△PAO中,PO=PA·sinα,

∴PO=.

    测量方法三:

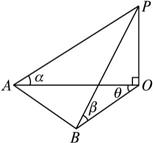
    在地面上引一条基线AB,这一基线与塔底在同一水平面上,且AB不过点O.测出AB的长、张角∠AOB(设为θ)及A、B对塔顶P的仰角α、β,则可求出铁塔PO的高.

    计算方法如下:

    如图所示,在Rt△POA中,AO=PO·cotα,

    在Rt△POB中,BO=PO·cotβ,

    在△AOB中,由余弦定理得

OA²+OB²-2OA·OB·cosθ=AB²,

∴PO=.