Question

（本小题满分12分）

设函数在及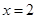时取得极值．

（I）求的值；

（II）若对于任意的，都有成立，求c的取值范围．

 

Answer 1

【答案】

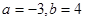（I）（II）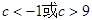

【解析】

试题分析：（I）由题意知，,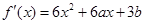

因为函数在及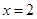时取得极值，所以及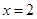是导函数的两个根,

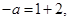
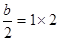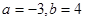由韦达定理知：，即.                      ……6分

（II）由（I）知，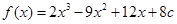

所以，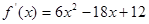

令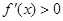得：，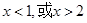

所以当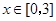时，函数在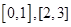上单调递增，在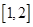上单调递减，      ……8分

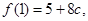
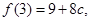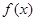又因为所以在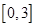上的最大值为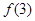，    ……10分

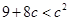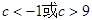所以，解得：.                                 ……12分

考点：本小题主要考查由导数研究函数的单调性、极值、最值和恒成立问题，考查学生的转化能力和运算求解能力.

点评：函数的极值点一定是导函数为零的点，但导函数为零的点不一定是极值点；根据函数的极值点和端点处的函数值进行比较，就能得出函数的最值，而恒成立问题一般转化为最值问题进行解决.