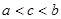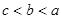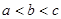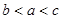题目内容
已知函数 (
(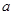 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当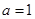 时,求
时,求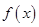 的单调区间;
的单调区间;
(2)若函数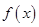 在
在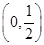 上无零点,求
上无零点,求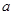 的最小值;
的最小值;
(3)若对任意的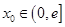 ,在
,在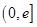 上存在两个不同的
上存在两个不同的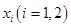 使得
使得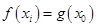 成立,求
成立,求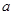 的取值范围.
的取值范围.
 (
(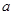 为常数,
为常数, 为自然对数的底)
为自然对数的底)(1)当
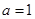 时,求
时,求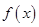 的单调区间;
的单调区间;(2)若函数
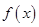 在
在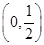 上无零点,求
上无零点,求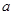 的最小值;
的最小值;(3)若对任意的
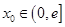 ,在
,在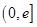 上存在两个不同的
上存在两个不同的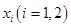 使得
使得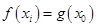 成立,求
成立,求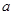 的取值范围.
的取值范围.(1)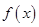 的减区间为
的减区间为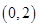 ,增区间为
,增区间为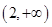 ;
;
(2)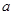 的最小值为
的最小值为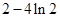 ;
;
(3)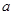 的取值范围是
的取值范围是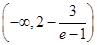 .
.
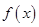 的减区间为
的减区间为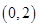 ,增区间为
,增区间为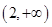 ;
;(2)
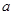 的最小值为
的最小值为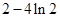 ;
;(3)
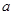 的取值范围是
的取值范围是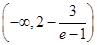 .
.试题分析:(1)将
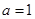 代入函数
代入函数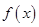 的解析式,利用导数求出
的解析式,利用导数求出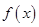 的单调递增区间和递减区间;(2)将函数
的单调递增区间和递减区间;(2)将函数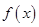 在
在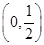 上无零点的问题转化为直线
上无零点的问题转化为直线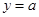 与曲线
与曲线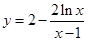 在区间
在区间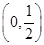 上无交点,利用导数确定函数
上无交点,利用导数确定函数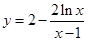 在区间
在区间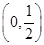 上的图象,进而求出参数
上的图象,进而求出参数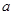 的取值范围,从而确定
的取值范围,从而确定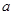 的最小值;(3)先研究函数
的最小值;(3)先研究函数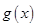 在
在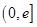 上的单调性,然后再将题干中的条件进行适当转化,利用两个函数的最值或端点值进行分析,列出相应的不等式,从而求出
上的单调性,然后再将题干中的条件进行适当转化,利用两个函数的最值或端点值进行分析,列出相应的不等式,从而求出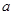 的取值范围.
的取值范围.试题解析:(1)
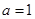 时,
时,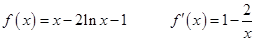
由
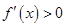 得
得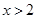
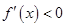 得
得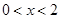
故
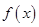 的减区间为
的减区间为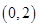 增区间为
增区间为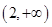 3分
3分(2)因为
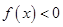 在
在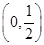 上恒成立不可能
上恒成立不可能故要使
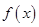 在
在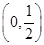 上无零点,只要对任意的
上无零点,只要对任意的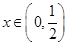 ,
,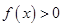 恒成立
恒成立即
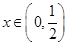 时,
时,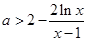 5分
5分令
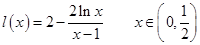
则
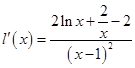
再令
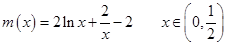
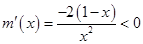 于是在
于是在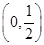 上
上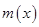 为减函数
为减函数故
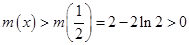
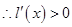 在
在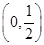 上恒成立
上恒成立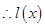 在
在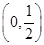 上为增函数
上为增函数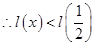 在
在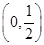 上恒成立
上恒成立又
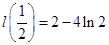
故要使
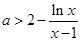 恒成立,只要
恒成立,只要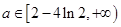
若函数
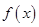 在
在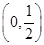 上无零点,
上无零点,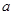 的最小值为
的最小值为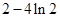 8分
8分(3)
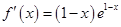
当
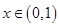 时,
时,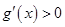 ,
,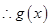 为增函数
为增函数当
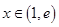 时,
时,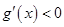 ,
,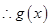 为减函数
为减函数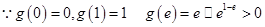
 函数
函数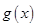 在
在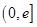 上的值域为
上的值域为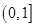 9分
9分当
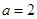 时,不合题意
时,不合题意当
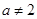 时,
时,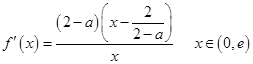
故
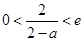
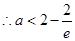 ① 10分
① 10分此时,当
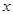 变化时,
变化时,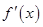 ,
,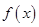 的变化情况如下
的变化情况如下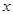 | 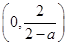 |  |  |
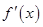 | — | 0 | + |
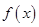 | ↘ | 最小值 | ↗ |
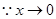 时,
时,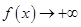 ,
,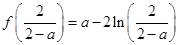
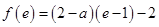
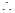 任意定的
任意定的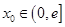 ,在区间
,在区间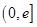 上存在两个不同的
上存在两个不同的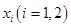
使得
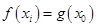 成立,
成立,当且仅当
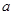 满足下列条件
满足下列条件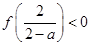 即
即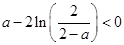 ②
②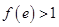 即
即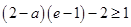 ③ 11分
③ 11分令
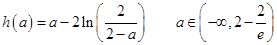
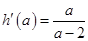 令
令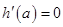 得
得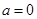
当
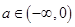 时,
时,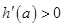 函数
函数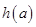 为增函数
为增函数当
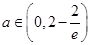 时,
时,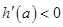 函数
函数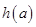 为减函数
为减函数所以在任取
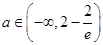 时有
时有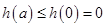
即②式对
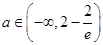 恒成立 13分
恒成立 13分由③解得
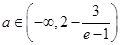 ④
④由①④ 当
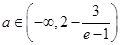 时
时对任意
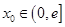 ,在
,在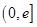 上存在两个不同的
上存在两个不同的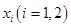 使
使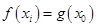 成立
成立
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
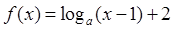 的图象恒过定点( )
的图象恒过定点( )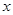 、
、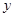 ,则
,则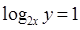 的概率为
的概率为  (其中
(其中 为常数且
为常数且 ),满足
),满足 ,则
,则 的解集是 .
的解集是 . ,则a的取值范围为( )
,则a的取值范围为( ) )
) 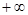 )
) (1,
(1,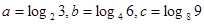 ,则
,则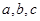 的大小关系是 .
的大小关系是 .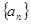 为各项为正数的等比数列,且
为各项为正数的等比数列,且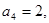 已知函数
已知函数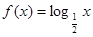 ,则
,则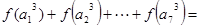
 的值为( )
的值为( )


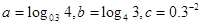 ,则( )
,则( )