题目内容
12.定义运算a⊕b=a2+2ab-b2,则cos$\frac{π}{6}$⊕sin$\frac{π}{6}$=$\frac{1+\sqrt{3}}{2}$.分析 利用新定义,特殊角的三角函数值,求得要求式子的值.
解答 解:∵运算a⊕b=a2+2ab-b2,则cos$\frac{π}{6}$⊕sin$\frac{π}{6}$=${cos}^{2}\frac{π}{6}$+2cos$\frac{π}{6}$sin$\frac{π}{6}$-${sin}^{2}\frac{π}{6}$=$\frac{3}{4}$+2•$\frac{\sqrt{3}}{2}•\frac{1}{2}$-$\frac{1}{4}$=$\frac{1+\sqrt{3}}{2}$,
故答案为:$\frac{{1+\sqrt{3}}}{2}$.
点评 本题主要考查新定义,特殊角的三角函数值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
 如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )| A. | $\frac{π}{2}-\frac{{\sqrt{3}}}{8}$ | B. | $\frac{π}{2}-\frac{{3\sqrt{3}}}{8}$ | C. | $\frac{3π}{2}-\frac{{\sqrt{3}}}{8}$ | D. | $\frac{3π}{2}-\frac{{3\sqrt{3}}}{8}$ |
3.已知点A(-1,0),B(1,0)为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-y2=1 | D. | x2-$\frac{{y}^{2}}{2}$=1 |
20.用反证法证明命题:“若a,b∈Z,ab能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A. | a,b都能被5整除 | B. | a,b都不能被5整除 | ||
| C. | a,b有一个能被5整除 | D. | a,b有一个不能被5整除 |
17.与两个相交平面的交线平行的直线和这两个平面的位置关系是( )
| A. | 都平行 | B. | 都相交 | ||
| C. | 在两平面内 | D. | 至少和其中一个平行 |
1.若|$\frac{x}{x+1}$|>$\frac{x}{x+1}$则实数x的取值范围是( )
| A. | (-1,0) | B. | [-1,0] | C. | (-∞,-1)∪(0,+∞) | D. | (-∞,-1]∪[0,+∞) |
2.甲、乙两台自动车床生产同种标准件,ξ表示甲机床生产1000件产品中的次品数,η表示乙机床生产1000件产品中的次品数,经过一段时间的测试,ξ与η的分布列分别为:
据此判定( )
| ζ | 0 | 1 | 2 | 3 |
| P | 0.7 | 0.1 | 0.1 | 0.1 |
| η | 0 | 1 | 2 | 3 |
| p | 0.5 | 0.3 | 0.2 | 0 |
| A. | 甲比乙质量好 | B. | 乙比甲质量好 | C. | 甲与乙质量相同 | D. | 无法判定 |
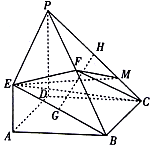 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.