题目内容
设函数 的定义域为
的定义域为 ,值域为[1,4].
,值域为[1,4].(1)求m,n的值;
(2)若f(x)=2,求x的值.
【答案】分析:(1)先根据两角和与差的公式进行化简,再由x的范围确定2x+ 的范围,再由余弦函数的性质表示出函数f(x)的值域,进而可确定m,n的值.
的范围,再由余弦函数的性质表示出函数f(x)的值域,进而可确定m,n的值.
(2)根据(1)求得函数f(x)的解析式,然后令f(x)=2,根据余弦函数的性质得到x的值.
解答:解:(1)
= .
.
∵ ,
,
∴
 ,
,
∵m>0, ,
,
所以f(x)max=2m+n=4,
f(x)min=-m+n=1,
m=1,n=2
(2)由(1)可知,m>0时,
 所以
所以 ,结合定义域为
,结合定义域为 ,
,
解得 .
.
点评:本题主要考查两角和与差的公式的应用和余弦函数的值域的求法.考查对余弦函数的简单应用.三角函数的基本性质是高考中的重要考点,要注意复习.
 的范围,再由余弦函数的性质表示出函数f(x)的值域,进而可确定m,n的值.
的范围,再由余弦函数的性质表示出函数f(x)的值域,进而可确定m,n的值.(2)根据(1)求得函数f(x)的解析式,然后令f(x)=2,根据余弦函数的性质得到x的值.
解答:解:(1)

=
 .
.∵
 ,
,∴

 ,
,∵m>0,
 ,
,所以f(x)max=2m+n=4,
f(x)min=-m+n=1,
m=1,n=2
(2)由(1)可知,m>0时,
 所以
所以 ,结合定义域为
,结合定义域为 ,
,解得
 .
.点评:本题主要考查两角和与差的公式的应用和余弦函数的值域的求法.考查对余弦函数的简单应用.三角函数的基本性质是高考中的重要考点,要注意复习.

练习册系列答案
相关题目
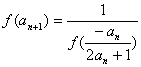 (n∈N*)
(n∈N*) .
. 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围.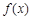 的定义域为
的定义域为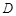 ,若存在非零实数
,若存在非零实数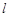 使得对于任意
使得对于任意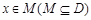 ,有
,有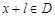 ,且
,且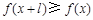 ,则称
,则称 上的
上的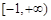 的函数
的函数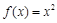 为
为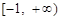 上的
上的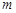 高调函数,那么实数
高调函数,那么实数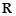 的函数
的函数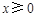 时,
时,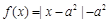 ,且
,且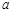 的取值范围是 .
的取值范围是 .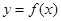 的定义域为R,当
的定义域为R,当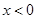 时,
时, ,且对任意实数
,且对任意实数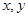 ,都有
,都有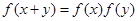 成立,数列
成立,数列 满足
满足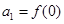 且
且
 的值;
的值;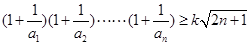 对一切
对一切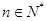 均成立,求
均成立,求 的最大值.
的最大值.