题目内容
2. 如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.
如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.(1)求λ的值;
(2)求二面角A1-BD-E的余弦值.
分析 (1)如图所示,以DA、DC所在直线分别为x,y轴,过点D作AA1的平行线为z轴,建立空间直角坐标系.AA1⊥平面ABCD,CE⊥平面ABCD,可得AA1∥CE∥z轴,又CE=λAA1,可得$\overrightarrow{DE}$=$\overrightarrow{DC}$+$λ\overrightarrow{A{A}_{1}}$=(0,2,4λ).由A1C⊥平面BED,可得$\overrightarrow{{A}_{1}C}•\overrightarrow{DE}$=0,解得$λ=\frac{1}{4}$.
(2)由于A1C⊥平面BED,可取$\overrightarrow{{A}_{1}C}$作为平面BED的法向量.设平面BDA1的法向量为$\overrightarrow{n}$=(x,y,z),利用$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=0}\\{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=0}\end{array}\right.$,可得取$\overrightarrow{n}$.利用$cos<\overrightarrow{n},\overrightarrow{{A}_{1}C}>$=$\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{n}}{|\overrightarrow{{A}_{1}C}||\overrightarrow{n}|}$即可得出.
解答 解:(1)如图所示,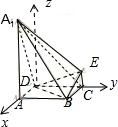 以DA、DC所在直线分别为x,y轴,过点D作AA1的平行线为z轴,建立空间直角坐标系.
以DA、DC所在直线分别为x,y轴,过点D作AA1的平行线为z轴,建立空间直角坐标系.
则D(0,0,0),B(2,2,0),C(0,2,0),A1(2,0,4),A(2,0,0).
$\overrightarrow{DB}$=(2,2,0),$\overrightarrow{{A}_{1}C}$=(-2,2,-4),
∵AA1⊥平面ABCD,CE⊥平面ABCD,∴AA1∥CE∥z轴,
又CE=λAA1,∴$\overrightarrow{DE}$=$\overrightarrow{DC}$+$λ\overrightarrow{A{A}_{1}}$=(0,2,4λ).
∵A1C⊥平面BED,∴$\overrightarrow{{A}_{1}C}⊥\overrightarrow{DE}$,∴$\overrightarrow{{A}_{1}C}•\overrightarrow{DE}$=4-16λ=0,解得$λ=\frac{1}{4}$.
(2)∵A1C⊥平面BED,∴可取$\overrightarrow{{A}_{1}C}$=(-2,2,-4)作为平面BED的法向量.
$\overrightarrow{D{A}_{1}}$=(2,0,4),
设平面BDA1的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=0}\\{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x+2y=0}\\{2x+4z=0}\end{array}\right.$,取$\overrightarrow{n}$=(2,-2,-1).
∴$cos<\overrightarrow{n},\overrightarrow{{A}_{1}C}>$=$\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{n}}{|\overrightarrow{{A}_{1}C}||\overrightarrow{n}|}$=$\frac{-4}{\sqrt{24}•\sqrt{9}}$=-$\frac{\sqrt{6}}{9}$.
∴二面角A1-BD-E(为钝角)的余弦值为$-\frac{\sqrt{6}}{9}$.
点评 本题考查了线面垂直的判定与性质定理、向量与数量积的关系、利用法向量求空间角,考查了推理能力与计算能力,属于中档题.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
| A. | λ<0 | B. | λ=0 | C. | 0<λ<1 | D. | λ>1 |
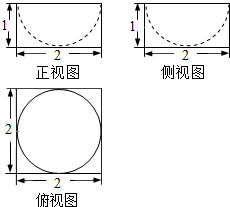
| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |