题目内容
如图,VC是△ABC所在平面的斜线,V在面ABC上的射影为N,N在△ABC的高CD上,M是VC上的一点,∠MDC=∠CVN.求证:VC⊥面AMB.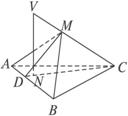
证明:∵VN⊥面ABC,CD⊥AB,且N在CD上,
∴由三垂线定理知AB⊥VC.又∵VN⊥平面ABC,∴VN⊥DN.
∵∠MDC=∠CVN,且∠VCD=∠VCD,∴∠DMC=∠VNC=90°,
即VC⊥DM.又∵AB∩DM=D,∴VC⊥平面ABM.
练习册系列答案
导学教程高中新课标系列答案
相关题目
导学教程高中新课标系列答案
19、如图已知VC是△ABC所在平面的一条斜线，点N是V在平面ABC上的射影，且在△ABC的高CD上．AB=a，VC与AB之间的距离为h，点M∈VC．
