已知函数f(x)=x3-3ax2+2bx在点x=1处有极小值-1.试求a.b的值.并求出f(x)的单调区间. 题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f(x)=x³-3ax²+2bx在点x=1处有极小值-1，试求a、b的值，并求出f(x)的单调区间.

解析：本题主要是考查函数和函数极值的概念、方程组和不等式的基本解法、运用导数研究函数性质的方法，同时考查运算能力和推理能力.为了加强对能力的考查，本题给出的函数f(x)中设置了参变量a、b，并将题设条件改为已知函数的极值点.要求首先求出参变量(待定系数)，再进行求导运算，求出f(x)的单调区间.这样的题目设置使试题具有一定的综合性，能较好地实现对能力的考查，区分出不同水平的考生.

答案：由已知可得f(1)=1-3a+2b=-1, ①?

又f′(x)=3x²-6ax+2b,∴f′(1)=3-6a+2b=0. ②?

由①②联立可得

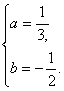∴故函数的解析式为f(x)=x³-x²-x,由此得f′(x)=3x²-2x-1.?

根据二次函数的性质，?

当x＜-或x＞1时，f′(x)＞0;?

当-＜x＜1时,f′(x)＜0.?

因此,在区间(-∞,- )和(1,+∞)上函数f(x)为增函数,在区间(-,1)内函数f(x)为减函数.

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

（2011•上海模拟）已知函数f(x)=(

-1)2+(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

4c2

k(k+c)

．

已知函数f(x)的图像在[a，b]上连续不断，f₁(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f₂(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f₂(x)－f₁(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x²，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．

已知函数f（x）、g（x），下列说法正确的是（）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

试题分类