题目内容
等差数列{an}的前n项和为Sn,a2,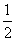 a4,a7-1成等比数列,且S15=0,求数列{an}的通项公式.
a4,a7-1成等比数列,且S15=0,求数列{an}的通项公式.
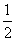 a4,a7-1成等比数列,且S15=0,求数列{an}的通项公式.
a4,a7-1成等比数列,且S15=0,求数列{an}的通项公式. 解:设等差数列{an}的公差为d,
由题设,有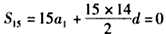 ,即
,即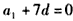 ,①
,①
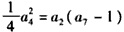 ,
,
即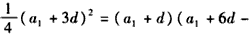
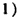 ,②
,②
由①、②得a1=0,d=0或a1=21,d=-3;
当a1=0,d=0时,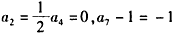 与题设矛盾;
与题设矛盾;
经检验,a1=21,d=-3合乎题设,
所以an=21-3(n-1)=24-3n。
由题设,有
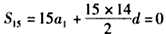 ,即
,即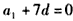 ,①
,①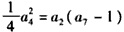 ,
,即
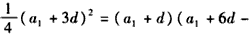
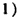 ,②
,② 由①、②得a1=0,d=0或a1=21,d=-3;
当a1=0,d=0时,
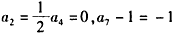 与题设矛盾;
与题设矛盾;经检验,a1=21,d=-3合乎题设,
所以an=21-3(n-1)=24-3n。

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |