题目内容
直线l过抛物线C: x2=4y的焦点且与y轴垂直，则l与C所围成的图形的面积等于（ ）
A．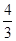
B．2 C．
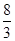D．
【答案】
C
【解析】直线l的方程为
，由
得交点坐标
，
，故l与C所围成的图形的面积为
.
【考点定位】本小题考查了直线和抛物线的位置关系、定积分的计算及其应用.
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
直线l过抛物线C：y2=2px（p＞0）的焦点F，且交抛物线C于A，B两点，分别从A，B两点向抛物线的准线引垂线，垂足分别为A1，B1，则∠A1FB1是（ ）
| A、锐角 | B、直角 | C、钝角 | D、直角或钝角 |
已知直线l过抛物线C的焦点，且与C的对称轴垂直．l与C交于A，B两点，|AB|=12，P为C的准线上一点，则△ABP的面积为（ ）
| A、18 | B、24 | C、36 | D、48 |