题目内容
(本小题满分12分) 过圆 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于 的对称点为E,关于
的对称点为E,关于 的对称点为F,求|EF|的取值范围.
的对称点为F,求|EF|的取值范围.
【答案】
(1)连结PC,由垂径分弦定理知,PC⊥AB,所以点P的轨迹是以线段AC为直径的圆(除去点A).因为点A(4,6),C(6,4),则其中点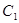 坐标为(5,5),又圆半径
坐标为(5,5),又圆半径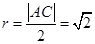 .
.
故点P的轨迹方程是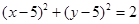 (x≠4,y≠6).(4分)
(x≠4,y≠6).(4分)
(2)设点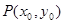 ,因为点P、E关于x=1对称,,则点
,因为点P、E关于x=1对称,,则点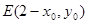
因为P、F关于y=x对称,则点F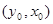 (6分)
(6分)
所以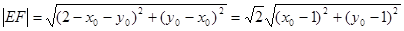
设点M(1,1),则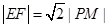 .
. 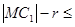
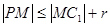
即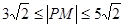 ,所以
,所以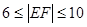 (12分)
(12分)
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目