题目内容
(本题满分12分)如图,在平面直坐标系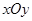 中,已知椭圆
中,已知椭圆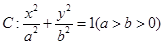 ,经过点
,经过点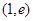 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆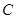 与直线
与直线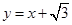 有且只有一个交点。
有且只有一个交点。
(Ⅰ)求椭圆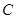 的方程;
的方程;
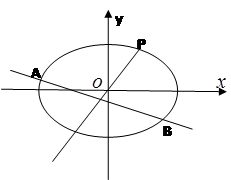
(Ⅱ)设不经过原点的直线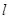 与椭圆
与椭圆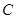 相交与A,B两点,第一象限内的点
相交与A,B两点,第一象限内的点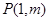 在椭圆上,直线
在椭圆上,直线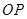 平分线段
平分线段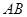 ,求:当
,求:当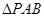 的面积取得最大值时直线
的面积取得最大值时直线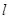 的方程。
的方程。
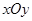 中,已知椭圆
中,已知椭圆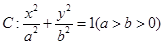 ,经过点
,经过点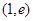 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆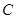 与直线
与直线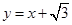 有且只有一个交点。
有且只有一个交点。
(Ⅰ)求椭圆
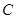 的方程;
的方程;(Ⅱ)设不经过原点的直线
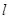 与椭圆
与椭圆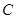 相交与A,B两点,第一象限内的点
相交与A,B两点,第一象限内的点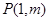 在椭圆上,直线
在椭圆上,直线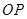 平分线段
平分线段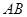 ,求:当
,求:当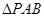 的面积取得最大值时直线
的面积取得最大值时直线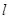 的方程。
的方程。(Ⅰ)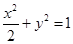 ;(Ⅱ)
;(Ⅱ)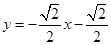 。
。
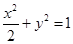 ;(Ⅱ)
;(Ⅱ)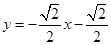 。
。试题分析:(Ⅰ)∵椭圆经过点
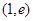 ,∴
,∴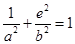 又
又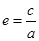 ,
,∴
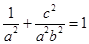 ,∴
,∴
∴椭圆的方程为
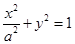 …………………………………………2分
…………………………………………2分又∵椭圆
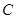 与直线
与直线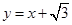 有且只有一个交点
有且只有一个交点∴方程
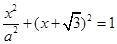 即
即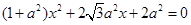 有相等实根
有相等实根∴
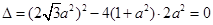 ∴
∴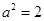
∴椭圆的方程为
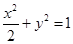 ………………………………………………5分
………………………………………………5分(Ⅱ)由(Ⅰ)知椭圆的方程为
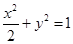 故
故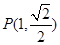
设不经过原点的直线
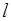 的方程
的方程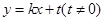 交椭圆
交椭圆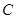 于
于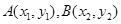
由
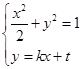 得
得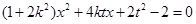 ……………………………6分
……………………………6分∴
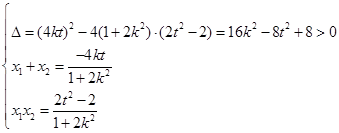 ………………7分
………………7分 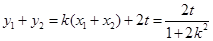
直线
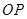 方程为
方程为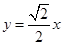 且
且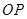 平分线段
平分线段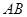
∴
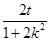 =
=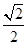
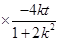 解得
解得 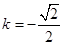 ……………………………………………8分
……………………………………………8分∴
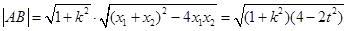
又∵点
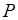 到直线
到直线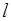 的距离
的距离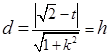
∴
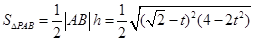 …………………………………………9分
…………………………………………9分设
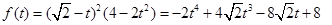
由直线
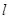 与椭圆
与椭圆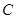 相交于A,B两点可得
相交于A,B两点可得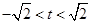
求导可得
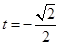
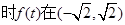
 ,此时
,此时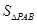 取得最大值
取得最大值此时直线
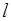 的方程
的方程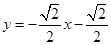 ……………………………………………12分
……………………………………………12分点评:求椭圆的标准方程是解析几何的基本问题,涉及直线与椭圆的位置关系问题,常常运用韦达定理,本题属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
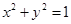 和定点A(2,1),由圆O外一点
和定点A(2,1),由圆O外一点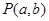 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足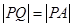
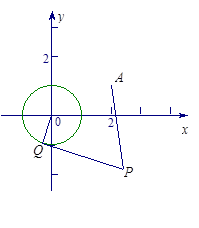
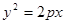 的焦点与双曲线
的焦点与双曲线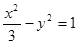 的左焦点重合,则实数
的左焦点重合,则实数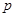 = .
= . 的左、右焦点为
的左、右焦点为 、
、 ,直线x=m过
,直线x=m过 的面积等于 .
的面积等于 .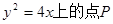 到抛物线的准线距离为d1,到直线
到抛物线的准线距离为d1,到直线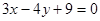 的距离为d2,则d1+d2的最小值是
的距离为d2,则d1+d2的最小值是  的一个焦点为
的一个焦点为 ,点
,点 在椭圆
在椭圆 上,点
上,点 满足
满足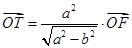 (其中
(其中 为坐标原点),过点
为坐标原点),过点 作一直线交椭圆于
作一直线交椭圆于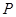 、
、 两点 .
两点 . 面积的最大值;
面积的最大值; 为点
为点 轴的对称点,判断
轴的对称点,判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由. 在曲线
在曲线 上,点
上,点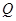 在曲线
在曲线 上,则
上,则 的最小值等于 .
的最小值等于 .
 与圆
与圆 (
( 为椭圆半焦距)有四个不同交点,则离心率的取值范围是 ( )
为椭圆半焦距)有四个不同交点,则离心率的取值范围是 ( )



 经过点
经过点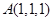 ,且
,且 是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面