题目内容
已知等差数列{an}中,a3+a7<2a6且a3,a7是方程x2-18x+65=0的两根,数列{bn}的前项和Sn=1-bn。
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项的和Tn,并证明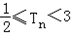 。
。
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项的和Tn,并证明
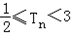 。
。解:(1)由a3+a7=2a5<2a6得a5<a6,
所以数列{an}是递增数列
所以a3<a7
由x2-18x+65=0解得a3=5,a7=13
公差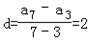 ,
,
所以an=a3+(n-3)d=2n-1(n∈N*)
由Sn=1-bn得,当n=1时,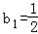 ;
;
当n≥2时,bn=Sn-Sn-1,得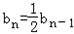
所以{bn}是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以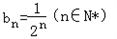 。
。
(2)证明:由(1)得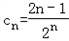 ,
,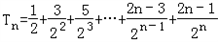
所以由错位相减法得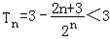
因为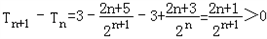
所以{Tn}是递增数列,所以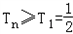
故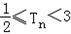 。
。
所以数列{an}是递增数列
所以a3<a7
由x2-18x+65=0解得a3=5,a7=13
公差
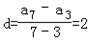 ,
,所以an=a3+(n-3)d=2n-1(n∈N*)
由Sn=1-bn得,当n=1时,
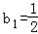 ;
;当n≥2时,bn=Sn-Sn-1,得
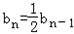
所以{bn}是首项为
 ,公比为
,公比为 的等比数列,
的等比数列,所以
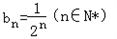 。
。(2)证明:由(1)得
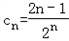 ,
,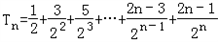
所以由错位相减法得
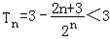
因为
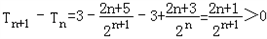
所以{Tn}是递增数列,所以
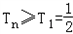
故
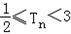 。
。
练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.