题目内容
(此题8、9、10班做)(本小题满分13分)
设数列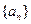 的前
的前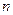 项和为
项和为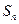 ,对一切
,对一切 ,点
,点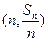 都在函数
都在函数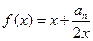 的图象上.
的图象上.
(Ⅰ)求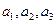 及数列
及数列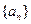 的通项公式
的通项公式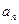 ;
;
(Ⅱ) 将数列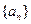 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(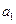 ),(
),(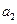 ,
,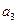 ),(
),(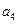 ,
,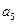 ,
,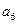 ),(
),(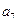 ,
,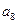 ,
,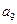 ,
,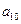 );(
);(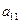 ),(
),(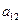 ,
,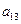 ),(
),(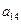 ,
,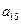 ,
,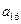 ),(
),(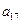 ,
,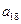 ,
, ,
,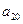 );(
);(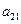 ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求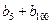 的值;
的值;
(Ⅲ)令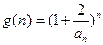 (
(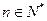 ),求证:
),求证: .
.
解:(Ⅰ)如果随机抽查这个班的一名学生,抽到积极参加班级工作的学生的概率是 ,所以积极参加班级工作的学生有
,所以积极参加班级工作的学生有 人,以此可以算出学习积极性一般且积极参加班级工作的人数为6,不太主动参加班级共工作的人数为26,学习积极性高但不太主动参加班级工作得人数为7,学习积极性高的人数为25,学习积极性一边拿的人数为25,得到变革如下:………………………………………………6分
人,以此可以算出学习积极性一般且积极参加班级工作的人数为6,不太主动参加班级共工作的人数为26,学习积极性高但不太主动参加班级工作得人数为7,学习积极性高的人数为25,学习积极性一边拿的人数为25,得到变革如下:………………………………………………6分 积极参加班级工作 不太主动参加班级工作 合计 学习积极性高 18 7 25 学习积极性一般 6 19 25 合计 24 26 50
(Ⅱ) ==≈11.5,
==≈11.5,
∵ >10.828,∴有99.9%的把握认为学习积极性与对待班级工作的态度有关系.………12分
>10.828,∴有99.9%的把握认为学习积极性与对待班级工作的态度有关系.………12分
解析

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上.
的图象上.  及数列
及数列 ;
; ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;
的值; (
( ),求证:
),求证: .
.