题目内容
已知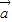 ,
,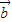 是单位向量,且
是单位向量,且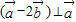 ,则
,则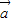 与
与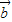 的夹角是( )
的夹角是( )A.
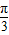
B.
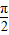
C.
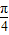
D.
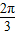
【答案】分析:设向量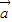 与
与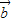 的夹角为θ,可得
的夹角为θ,可得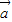 •
•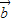 =cosθ,再根据
=cosθ,再根据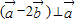 ,得2cosθ-1=0,最后结合θ∈[0,π],可得向量
,得2cosθ-1=0,最后结合θ∈[0,π],可得向量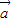 与
与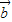 的夹角的大小.
的夹角的大小.
解答:解:设向量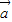 与
与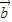 的夹角为θ,
的夹角为θ,
∴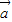 •
•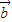 =|
=|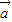 |•|
|•|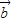 |cosθ=1×1×cosθ=cosθ
|cosθ=1×1×cosθ=cosθ
∵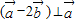 ,
,
∴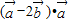 =
=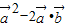 =0,得2cosθ-1=0,所以cosθ=
=0,得2cosθ-1=0,所以cosθ= ,
,
∵θ∈[0,π],∴θ=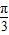 .
.
故选A.
点评:本题着重考查了平面向量的数量积与向量的垂直关系的应用,求解向量的夹角的知识,属于基础题.
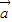 与
与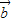 的夹角为θ,可得
的夹角为θ,可得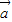 •
•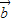 =cosθ,再根据
=cosθ,再根据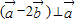 ,得2cosθ-1=0,最后结合θ∈[0,π],可得向量
,得2cosθ-1=0,最后结合θ∈[0,π],可得向量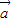 与
与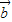 的夹角的大小.
的夹角的大小.解答:解:设向量
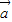 与
与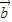 的夹角为θ,
的夹角为θ,∴
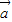 •
•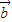 =|
=|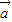 |•|
|•|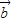 |cosθ=1×1×cosθ=cosθ
|cosθ=1×1×cosθ=cosθ∵
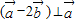 ,
,∴
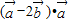 =
=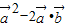 =0,得2cosθ-1=0,所以cosθ=
=0,得2cosθ-1=0,所以cosθ= ,
,∵θ∈[0,π],∴θ=
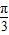 .
.故选A.
点评:本题着重考查了平面向量的数量积与向量的垂直关系的应用,求解向量的夹角的知识,属于基础题.

练习册系列答案
相关题目
 都是单位向量,且
都是单位向量,且 ,则
,则 的值为 .
的值为 . 都是单位向量,且
都是单位向量,且 ,则
,则 的值为 .
的值为 .