题目内容
设函数f（x）=（1+x）2+ln（1+x）2．
（1）求f（x）的单调区间；
（2）若当x∈[
﹣1，e﹣1]时，不等式f（x）＜m恒成立，求实数m的取值范围；
（3）若关于x的方程f（x）=x2+x+a在区间[0，2]上恰好有两个相异的实根，求实数a的取值范围．
考点：
利用导数研究函数的单调性；函数与方程的综合运用；利用导数求闭区间上函数的最值．
专题：
综合题；压轴题；导数的综合应用．
分析：
（1）确定函数定义域，求导函数，利用导数的正负，可得f（x）的单调区间；
（2）确定函数在[﹣1，e﹣1]上的单调性，从而可得函数的最大值，不等式，即可求得实数m的取值范围；
（3）方程f（x）=x2+x+a，即x﹣a+1﹣ln（1+x）2=0，记g（x）=x﹣a+1﹣ln（1+x）2．求导函数，确定函数在区间[0，2]上的单调性，为使f（x）=x2+x+a在[0，2]上恰好有两个相异的实根，只须g（x）=0在[0，1]和（1，2]上各有一个实根，从而可建立不等式，由此可求实数a的取值范围．
解答：
解：（1）函数定义域为（﹣∞，﹣1）∪（﹣1，+∞），
因为
=
，
由f′（x）＞0得﹣2＜x＜﹣1或x＞0，由f′（x）＜0得x＜﹣2或﹣1＜x＜0．
∴函数的递增区间是（﹣2，﹣1），（0，+∞），递减区间是（﹣∞，﹣2），（﹣1，0）．
（2）由f′（x）==0得x=0或x=﹣2．由（1）知，f（x）在[﹣1，0]上递减，在[0，e﹣1]上递增．
又f（﹣1）=
+2，f（e﹣1）=e2﹣2，
∴
=
＞0
∴e2﹣2＞+2．所以x∈[
﹣1，e﹣1]时，[f（x）]max=e2﹣2．故m＞e2﹣2时，不等式f（x）＜m恒成立．
（3）方程f（x）=x2+x+a，即x﹣a+1﹣ln（1+x）2=0，记g（x）=x﹣a+1﹣ln（1+x）2．
所以g′（x）=1﹣
=
．
由g′（x）＞0，得x＜﹣1或x＞1，由g′（x）＜0，得﹣1＜x＜1．
所以g（x）在[0，1]上递减，在[1，2]上递增，
为使f（x）=x2+x+a在[0，2]上恰好有两个相异的实根，只须g（x）=0在[0，1]和（1，2]上各有一个实根，于是有
，∴
，
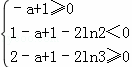∴2﹣2ln2＜a≤3﹣2ln3．
点评：
本题考查导数知识的运用，考查函数的单调性，考查恒成立问题，考查函数与方程思想，属于中档题．
