题目内容
【题目】已知函数![]() 的极小值为
的极小值为![]() ,其导函数
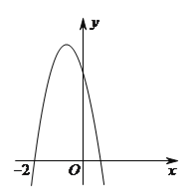
,其导函数![]() 的图象经过点
的图象经过点![]() ,如图所示.
,如图所示.
(Ⅰ)求![]() 的解析式.
的解析式.
(Ⅱ)若函数![]() 在区间
在区间![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】试题分析:(Ⅰ)求出y=f'(x),因为导函数图象经过(-2,0),代入即可求出a、b之间的关系式,再根据f(x)极小值为-8可得f(-2)=-8,解出即可得到a、b的值;
(Ⅱ)将函数g(x)=f(x)-k在区间[-3,2]上有两个不同的零点,转化成k=f(x)在区间[-3,2]上有两个不同的根,即y=k与y=f(x)的图象在区间[-3,2]上有两个不同的交点,列出表格,即可求出实数k的取值范围.
试题解析:
(Ⅰ)∵![]() ,
,
由题可知: 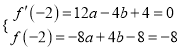 ,
,
解得![]() ,
, ![]() ,
,
∴![]() .
.
(Ⅱ)∵![]() 在区间
在区间![]() 上有两个不同零点,
上有两个不同零点,
∴![]() 在
在![]() 上有两个不同的根,
上有两个不同的根,
即![]() 与
与![]() 在
在![]() 上有两个不同的交点,
上有两个不同的交点,
![]() ,令
,令![]() ,
,
则![]() 或
或![]() ,列表可知,
,列表可知,
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
由表可知当![]() 或
或![]() 时,
时,
方程![]() 在
在![]() 上有两个不同的根,
上有两个不同的根,
即函数![]() 在区间上有两个不同的零点.
在区间上有两个不同的零点.

练习册系列答案
相关题目
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次 射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.


