题目内容
(12分)
是否存在常数a,b,使等式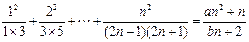 对于一切
对于一切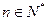 都成立?
都成立?
解:若存在常数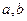 使等式成立,则将
使等式成立,则将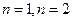 代入上式,有
代入上式,有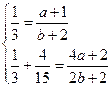
得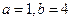 ,即有
,即有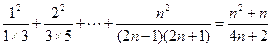 对于一切
对于一切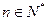 成立…………4分
成立…………4分
证明如下:
(1)当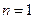 时,左边=
时,左边=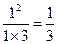 ,右边=
,右边=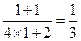 ,所以等式成立 …………6分
,所以等式成立 …………6分
(2)假设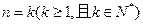 时等式成立,即
时等式成立,即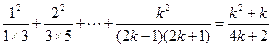
当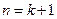 时,
时,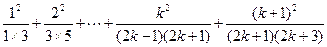 =
=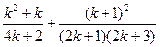
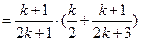 =
=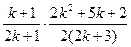 =
=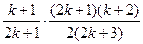
=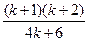 =
=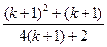
也就是说,当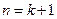
 时,等式成立, …………11分
时,等式成立, …………11分
综上所述,可知等式对任何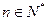 都成立。 …………12分
都成立。 …………12分
解析

练习册系列答案
相关题目