题目内容
已知数列{an}为等差数列,Sn为{an}的前几项和,{an}的公差为d.
(I)若{an}中,a2,S4,S5成等差数列,且a3,a4+1,S5-3成等比数列.求an.
(II)若d<0,试比较2Sn+Sn+2与4Sn+1的大小.
(I)若{an}中,a2,S4,S5成等差数列,且a3,a4+1,S5-3成等比数列.求an.
(II)若d<0,试比较2Sn+Sn+2与4Sn+1的大小.
分析:(I)利用等差数列和等比数列的通项公式及其前n项和公式即可得出;
(II)作商与1比较即可.
(II)作商与1比较即可.
解答:解:(I)设{an}的首项为a1公差为d,则an=a1+(n-1)d,Sn=na1+
n(n-1)d
依体意得
,
化为
,
解得:
或
,
∴an=2n-3或an=-
n+
(II)∵
=2(Sn+2-Sn+1)-(Sn+1-Sn)=2an+2-an+1=2d
∵d<0∴2d<1∴2Sn+Sn+2<4Sn+1.
| 1 |
| 2 |
依体意得
|
化为
|
解得:
|
|
∴an=2n-3或an=-
| 1 |
| 10 |
| 3 |
| 20 |
(II)∵
| 2Sn+Sn+2 |
| 4Sn+1 |
∵d<0∴2d<1∴2Sn+Sn+2<4Sn+1.
点评:熟练掌握等差数列和等比数列的通项公式及其前n项和公式、两个数比较大小的方法等是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

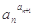 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4