题目内容
（本小题共12分）
甲、乙两个射手进行射击训练，甲击中目标的概率为
，乙击中目标的概率为
，每人各射击两发子弹为一个“单位射击组”，若甲击中目标的次数比乙击中目标的次数多，则称此组为“单位进步组”.
（1）求一个“单位射击组”为“单位进步组”的概率；
（2）记完成三个“单位射击组”后出现“单位进步组”的次数
，求的分布列与数学期望.
,
解析:
解：（1）设甲击中目标2次时为“单位进步组”的概率为
，
则
设甲击中目标1次时为“单位进步组”的概率为
，
则
．
故一个“单位射击组”成为“单位进步组”的概率为．
（2）由（1）知，一个“单位射击组”成为“单位进步组”的概率
不能成为“单位进步组”的概率
.
可能取值为0，1，2，3.
,
∴的分布列为
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
∴的数学期望．
（或
﹀
）
练习册系列答案
相关题目
的焦点坐
标为
（
），点M（
，
）在椭圆E上
（1）求椭圆E的方程；（2）O为坐标原点，⊙
的任意一条切线与椭圆E有两个交点
，
且
，求⊙
⊥平面
，
∥
是正三角形，
，且
是
的中点
∥平面
；
．
名，女同学有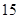
名，老师按照分层抽样的方法组建了一个
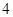人的课外兴趣小组．
名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
，
，求证：
.
的值.