题目内容
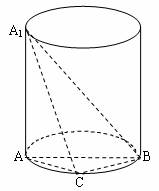
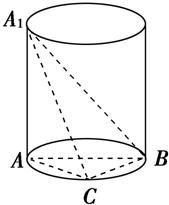 如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任=A意一点,A1A=AB=2.
如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任=A意一点,A1A=AB=2.(1)求证:BC⊥平面A1AC;
(2)求三棱锥A1-ABC的体积的最大值.
分析:(1)欲证BC⊥平面AA1C,根据直线与平面垂直的判定定理可知只需证BC与平面AA1C内两相交直线垂直,而BC⊥AC,AA1⊥BC,AA1∩AC=A满足定理条件;
(2)设AC=x,在Rt△ABC中,求出BC,根据体积公式VA1-ABC=
S△ABC•AA1表示成关于x的函数,根据二次函数求出其最大值.
(2)设AC=x,在Rt△ABC中,求出BC,根据体积公式VA1-ABC=
| 1 |
| 3 |
解答:解:(1)证明:∵C是底面圆周上异于A、B的任意一点,且AB是圆柱底面圆的直径,
∴BC⊥AC.
∵AA1⊥平面ABC,BC?平面ABC,
∴AA1⊥BC.
∵AA1∩AC=A,AA1?平面AA1C,AC?平面AA1C,
∴BC⊥平面AA1C.
(2)设AC=x,在Rt△ABC中,
BC=
=
(0<x<2),
故VA1-ABC=
S△ABC•AA1=
•
•AC•BC•AA1
=
x
(0<x<2),
即VA1-ABC=
x
=
=
.
∵0<x<2,0<x2<4,∴当x2=2,即x=
时,
三棱锥A1-ABC的体积最大,其最大值为
∴BC⊥AC.
∵AA1⊥平面ABC,BC?平面ABC,
∴AA1⊥BC.
∵AA1∩AC=A,AA1?平面AA1C,AC?平面AA1C,
∴BC⊥平面AA1C.
(2)设AC=x,在Rt△ABC中,
BC=
| AB2-AC2 |
| 4-x2 |
故VA1-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 4-x2 |
即VA1-ABC=
| 1 |
| 3 |
| 4-x2 |
| 1 |
| 3 |
| x2(4-x2) |
=
| 1 |
| 3 |
| -(x2-2)2+4 |
∵0<x<2,0<x2<4,∴当x2=2,即x=
| 2 |
三棱锥A1-ABC的体积最大,其最大值为
| 2 |
| 3 |
点评:本小题主要考查直线与平面垂直,以及棱柱、棱锥、棱台的体积等基础知识,考查空间想象能力,运算能力和推理论证能力.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
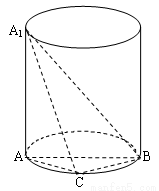
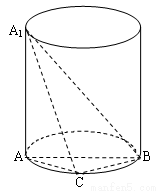
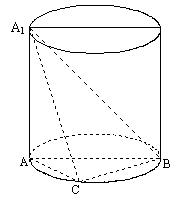
 (Ⅱ)求三棱锥A1-ABC的体积的最大值.
(Ⅱ)求三棱锥A1-ABC的体积的最大值.