题目内容
直线l经过点(1,1),若抛物线y2=x上存在两点关于直线l对称,求直线l斜率的取值范围.
解法一:设直线l的方程为y-1=k(x-1),弦的两个端点分别是A(x1,y1)、B(x2,y2),代入抛物线方程并作差得(y1+y2)(y1-y2)=x1-x2.
∵kAB=![]() =-
=-![]() ,
,
∴y1+y2=-k.注意到AB的中点在直线l:y-1=k(x-1)上,
∴x1+x2=1-![]() .
.
∴y12+y22=x1+x2=1-![]() .
.
由y12+y22>![]() ,得1-
,得1-![]() >
>![]()
![]()
![]() <0
<0![]() -2<k<0.
-2<k<0.
解法二:设抛物线上关于直线l:y-1=k(x-1)对称的两点为(y12,y1)、(y22,y2),则
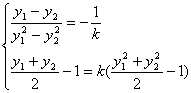
![]()
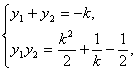
y1y2=![]() +
+![]() -
-![]() ,
,
∴y1、y2是方程y2+ky+![]() +
+![]() -
-![]() =0的两根.
=0的两根.
由Δ=k2-4(![]() +
+![]() -
-![]() )>0
)>0
![]()
![]() <0
<0
![]() -2<k<0.
-2<k<0.

练习册系列答案
相关题目