题目内容
如图，经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，则
∠BAC所对的弧的度数为
- A.40°
- B.100°
- C.120°
- D.30°
C
分析：由已知中经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，根据弦切角定理及三角形外角的性质，我们易求出∠BAC=60°，然后再利用圆周角定理，即可得到答案．
解答：∵PA为圆O的切线，
故∠CAP=∠B=40°，
又∵∠ACP=100°，
∴∠BAC=60°
则∠BAC所对的弧的度数为120°
故选C
点评：本题考查的知识点是弦切角定理，圆周角定理及三角形外角的性质，其中易忽略所求为∠BAC所对的弧的度数，而错答为60°．
分析：由已知中经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，根据弦切角定理及三角形外角的性质，我们易求出∠BAC=60°，然后再利用圆周角定理，即可得到答案．
解答：∵PA为圆O的切线，
故∠CAP=∠B=40°，
又∵∠ACP=100°，
∴∠BAC=60°
则∠BAC所对的弧的度数为120°
故选C
点评：本题考查的知识点是弦切角定理，圆周角定理及三角形外角的性质，其中易忽略所求为∠BAC所对的弧的度数，而错答为60°．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
9、如图，经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，则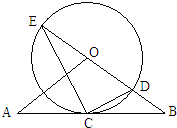
选修4-1：几何证明选讲
如图，直线D经过⊙O上的点C，并且OA=OB，CA=CB，直线OB交⊙O于点E、D，连接EC，CD．若tanE=