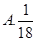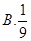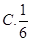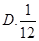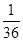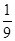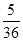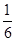题目内容
如图是某个四面体的三视图，若在该四面体的外接球内任取一点，则点落在四面体内的概率为（ ）
A． | B． | C． | D． |
C
解析试题分析：由题意可知三棱锥的底面是一个直角边为
等腰直角三角形，所以三棱锥的体积为12.球的直径
为三棱锥的三个两两垂直的棱为长方体的体对角线，即
.所以球的体积为
.所以点落在四面体内的概率为
.故选C.
考点：1.三视图的知识.2.球的内接几何体.3.概率问题.4.空间想象力.
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
设随机变量X～N(2，32)，若P(X≤c)＝P(X>c)，则c等于（ ）
| A．0 | B．1 | C．2 | D．3 |
在区间
上随机取一个实数
，使得
的概率为（ ）
A． | B． | C． | D． |
在区间
上随机取一个实数
，则事件：“
”的概率为（ ）
A． | B． | C． | D． |
容量为20的样本数据，分组后的频数如下表：
则样本数据落在区间［10,40）的频率为（ ）
| A．0.35 | B．0.45 | C．0.55 | D．0.65 |
