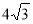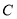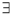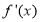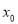题目内容
已知椭圆 :
: ,直线
,直线 交椭圆
交椭圆 于
于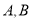 两点.
两点.
(Ⅰ)求椭圆 的焦点坐标及长轴长;
的焦点坐标及长轴长;
(Ⅱ)求以线段 为直径的圆的方程.
为直径的圆的方程.
(Ⅰ)焦点坐标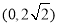 ,
,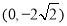 ,长轴长
,长轴长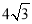 ;(Ⅱ)
;(Ⅱ)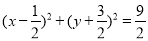
【解析】
试题分析:(Ⅰ)将椭圆方程变形为标准方程,即可知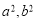 的值,根据
的值,根据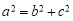 可求
可求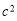 ,即可求出焦点坐标及长轴长。(Ⅱ)将直线和椭圆方程联立,消去
,即可求出焦点坐标及长轴长。(Ⅱ)将直线和椭圆方程联立,消去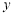 得关于
得关于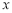 的一元二次方程,可求出两根,即为两交点的横坐标,分别代入直线方程可得交点的纵坐标。用中点坐标公式可求中点即圆心的坐标,再用两点间距离公式可求半径。
的一元二次方程,可求出两根,即为两交点的横坐标,分别代入直线方程可得交点的纵坐标。用中点坐标公式可求中点即圆心的坐标,再用两点间距离公式可求半径。
试题解析:【解析】
(Ⅰ)原方程等价于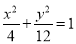 .
.
由方程可知: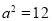 ,
,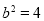 ,
,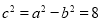 ,
,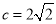 . 3分
. 3分
所以 椭圆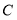 的焦点坐标为
的焦点坐标为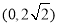 ,
,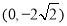 ,长轴长
,长轴长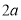 为
为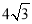 . 5分
. 5分
(Ⅱ)由 可得:
可得: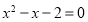 .
.
解得: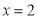 或
或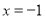 .
.
所以 点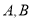 的坐标分别为
的坐标分别为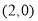 ,
,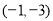 . 7分
. 7分
所以 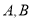 中点坐标为
中点坐标为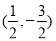 ,
,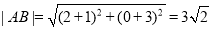 . 9分
. 9分
所以 以线段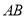 为直径的圆的圆心坐标为
为直径的圆的圆心坐标为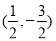 ,半径为
,半径为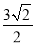 .
.
所以 以线段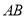 为直径的圆的方程为
为直径的圆的方程为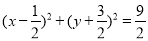 . 11分
. 11分
考点:1、椭圆的方程;2、直线与椭圆的相交弦问题;3、求圆的方程。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目