题目内容
(12分)已知椭圆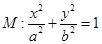
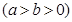 的离心率为
的离心率为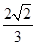 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为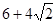 .
.
(1)求椭圆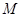 的方程;
的方程;
(2)设直线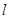 与椭圆
与椭圆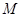 交于
交于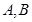 两点,且以
两点,且以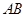 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点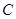 ,
,
求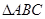 面积的最大值.
面积的最大值.
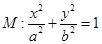
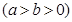 的离心率为
的离心率为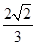 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为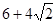 .
.(1)求椭圆
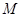 的方程;
的方程;(2)设直线
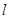 与椭圆
与椭圆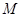 交于
交于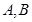 两点,且以
两点,且以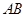 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点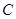 ,
,求
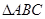 面积的最大值.
面积的最大值.(1) (2)
(2)
 (2)
(2)
试题分析:(Ⅰ)因为椭圆
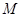 上一点和它的两个焦点构成的三角形周长为
上一点和它的两个焦点构成的三角形周长为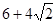 ,
,所以
 , 1分
, 1分又椭圆的离心率为
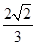 ,即
,即 ,所以
,所以 , 2分
, 2分所以
 ,
, . 4分
. 4分所以
 ,椭圆
,椭圆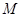 的方程为
的方程为 . 5分
. 5分(Ⅱ)不妨设
 的方程
的方程 ,则
,则 的方程为
的方程为 .
.由
 得
得 , 6分
, 6分设
 ,
, ,因为
,因为 ,所以
,所以 , 7分
, 7分同理可得
 , 8分
, 8分所以
 ,
, , 10分
, 10分 , 12分
, 12分设
 ,则
,则 , 13分
, 13分当且仅当
 时取等号,所以
时取等号,所以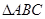 面积的最大值为
面积的最大值为 .
. 点评:直线与圆锥曲线相交,联立方程利用韦达定理是常用的思路

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
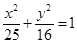 上的三点,点F(3,0),若
上的三点,点F(3,0),若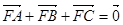 ,则
,则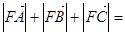
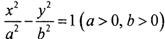 上•,
上•,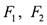 是这条双曲线的两个焦点,
是这条双曲线的两个焦点,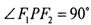 ,且
,且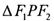 的三条边长成等差数列,则此双曲线的离心率是
的三条边长成等差数列,则此双曲线的离心率是 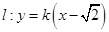 与双曲线
与双曲线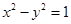 仅有一个公共点,则实数
仅有一个公共点,则实数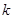 的值为
的值为 中的抛物线
中的抛物线 ,直线
,直线 过焦点
过焦点 且与抛物线相交于
且与抛物线相交于 ,
, 两点.
两点. 时,用
时,用 表示
表示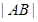 的长度;
的长度; 且三角形
且三角形 的面积为4时,求直线
的面积为4时,求直线 的渐近线方程是___________
的渐近线方程是___________ 中,双曲线
中,双曲线 的离心率为 .
的离心率为 . 的焦距是( )
的焦距是( )


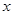 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为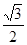 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为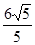 。
。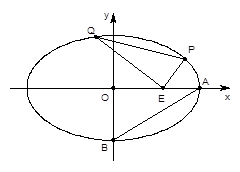
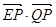 的取值范围.
的取值范围.