题目内容
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形
且∠A1AC=∠DAB=60o,平面AA1C1C⊥平面ABCD.(Ⅰ)证明:BD⊥AA1;
(Ⅱ)证明:平面AB1C∥平面DA1C1;
(Ⅲ)在棱CC1上是否存在点P,使得平面PDA1和平面DA1C1所成锐二面角的余弦值为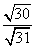 ?若存在,求出点P的位置;若不存在,说明理由.
?若存在,求出点P的位置;若不存在,说明理由.
 |
解:(Ⅰ)应选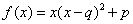 .
.
因为①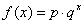 中单调函数;②
中单调函数;②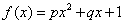 的图象不具有先升再降后升特征;③
的图象不具有先升再降后升特征;③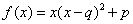 中,
中, ,令
,令 ,得
,得 ,
, ,
,
 有两个零点.出现两个递增区间和一个递减区间,符合价格走势;
有两个零点.出现两个递增区间和一个递减区间,符合价格走势;
(Ⅱ)由 ,
, ,得
,得 解得
解得 (其中
(其中 舍去)
舍去)
 ,即
,即 ;
;
(Ⅲ)由 ,解得
,解得 ,
,
| x | 0 | (0,1) | 1 | (1,3) | 3 | (3,5) | 5 |
|
| 6 | ↑ | 极大值 10 | ↓ | 极小值 6 | ↑ | 26 |
所以函数 在区间
在区间 上单调递减,
上单调递减,
故这种水果在5月,6月份价格下跌.且境外销售的价格为 (元)
(元)

练习册系列答案
相关题目
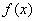
 :
: 的距离为 .
的距离为 . 在定义域
在定义域 内可导,其图象如下,记
内可导,其图象如下,记 ,则不等式
,则不等式 的解集为_________.
的解集为_________.
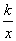 +
+ 在(1,+∞)上是增函数,则实数k的取值范围是( ).
在(1,+∞)上是增函数,则实数k的取值范围是( ). 上的奇函数,当
上的奇函数,当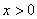 时,
时,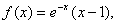 给出以下命题:
给出以下命题: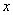
 时,
时,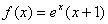 ; ②函数
; ②函数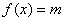 有解,则实数
有解,则实数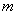 的取值范围是
的取值范围是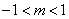 ;
;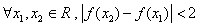 恒成立.
恒成立.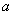 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值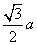 ,类比上述命题,棱长为
,类比上述命题,棱长为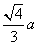 B.
B. C.
C. D.
D.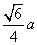
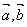 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么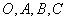 为空间四点,且向量
为空间四点,且向量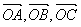 不构成空间的一个基底,则点
不构成空间的一个基底,则点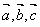 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底其中正确的命题是 ( )
也是空间的一个基底其中正确的命题是 ( ) ,则与其共线且满足
,则与其共线且满足 的向量
的向量 是 ( )
是 ( ) B.(4,-2,4) C.(-4,2,-4) D.(2,-3,4)
B.(4,-2,4) C.(-4,2,-4) D.(2,-3,4)