题目内容
一抛物线型拱桥,当水面离桥顶2m时,水面宽4m,若水面下降1m时,则水面宽为( )
A、
| ||
B、2
| ||
| C、4.5m | ||
| D、9m |
分析:建立适当的直角坐标系,设抛物线方程为x2=-2Py(P>0),由题意知抛物线过点(2,-2),进而求得p,得到抛物线的标准方程.进而可知当y0=-3时x02的值,最后根据水面宽为2|x0|求得答案.
解答:解:建立适当的直角坐标系,设抛物线方程为x2=-2Py(P>0),由题意知,抛物线过点(2,-2),
∴4=2p×2.∴p=1.∴x2=-2y.
当y0=-3时,得x02=6.
∴水面宽为2|x0|=2
.
∴4=2p×2.∴p=1.∴x2=-2y.
当y0=-3时,得x02=6.
∴水面宽为2|x0|=2
| 6 |
点评:本题主要考查了抛物线的性质.属基础题.

练习册系列答案
相关题目
 (从上游到下游标记,n=0,1,2……),经测量知,相邻两桥之间的距离
(从上游到下游标记,n=0,1,2……),经测量知,相邻两桥之间的距离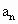 近似地满足
近似地满足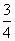 m,宽为4m.
m,宽为4m.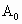 桥起锚顺水航行时,河水开始上涨,试问船将在哪一座桥可能受阻?(
桥起锚顺水航行时,河水开始上涨,试问船将在哪一座桥可能受阻?(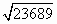 ≈153.9,
≈153.9,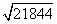 ≈147.8,
≈147.8,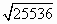 ≈159.9)
≈159.9)