题目内容
已知:一窗户满足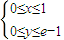 (单位m),一蜘蛛在窗户上布的蜘蛛网满足
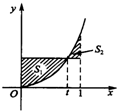
(单位m),一蜘蛛在窗户上布的蜘蛛网满足 (t为常数,且0≤t≤1),图象围成的封闭图形如图3中阴影所示.
(t为常数,且0≤t≤1),图象围成的封闭图形如图3中阴影所示.(1)当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值
(2)在(1)条件下若有4只苍蝇从窗户飞过,ξ表示蜘蛛捕捉到苍蝇数,求捕捉到苍蝇数分布列及数学期望.

【答案】分析:(1)窗户的最大面积是S1max=e-1,蜘蛛网的面积S2=∫t(et-ex)dx+∫t1(ex-et)dx=(2t-3)•et+e+1,t= 时,S2min=e-2
时,S2min=e-2 +1.所以当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值p=
+1.所以当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值p=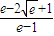 =
= .
.
(2)由题设知ξ~B(4, ),由此能求出ξ的分布列和Eξ.
),由此能求出ξ的分布列和Eξ.
解答:解:(1)∵一窗户满足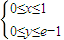 (单位m),
(单位m),
∴窗户的最大面积是S1max=e-1,
∵一蜘蛛在窗户上布的蜘蛛网满足 (t为常数,且0≤t≤1),
(t为常数,且0≤t≤1),
∴蜘蛛网的面积S2=∫t(et-ex)dx+∫t1(ex-et)dx
=[etx-ex]|t+[ex-etx]|t1
=et•t-et+1+e-et-et+ett
=2t•et-3et+e+1
=(2t-3)•et+e+1
∵S2′=2et+(2t-3)et,
∴由S2′=2et+(2t-3)et=0,得t= .
.
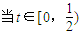 时,S2′=2et+(2t-3)et<0,
时,S2′=2et+(2t-3)et<0,
当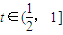 时,S2′=2et+(2t-3)et>0,
时,S2′=2et+(2t-3)et>0,
∴t= 时,S2min=e-2
时,S2min=e-2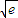 +1.
+1.
∴当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值
p=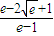 =
= .
.
(2)由题设知ξ~B(4,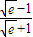 ),
),
∴ξ的分布列是P(ξ=k)=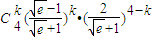 ,k=0,1,2,3,4.
,k=0,1,2,3,4.
Eξ=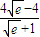 .
.
点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,注意定积分的灵活运用.计算量大且繁琐,容易出错,要注意培养计算能力.
 时,S2min=e-2
时,S2min=e-2 +1.所以当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值p=
+1.所以当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值p=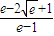 =
= .
.(2)由题设知ξ~B(4,
 ),由此能求出ξ的分布列和Eξ.
),由此能求出ξ的分布列和Eξ.解答:解:(1)∵一窗户满足
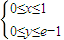 (单位m),
(单位m),∴窗户的最大面积是S1max=e-1,
∵一蜘蛛在窗户上布的蜘蛛网满足
 (t为常数,且0≤t≤1),
(t为常数,且0≤t≤1),∴蜘蛛网的面积S2=∫t(et-ex)dx+∫t1(ex-et)dx
=[etx-ex]|t+[ex-etx]|t1
=et•t-et+1+e-et-et+ett
=2t•et-3et+e+1
=(2t-3)•et+e+1
∵S2′=2et+(2t-3)et,
∴由S2′=2et+(2t-3)et=0,得t=
 .
.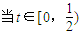 时,S2′=2et+(2t-3)et<0,
时,S2′=2et+(2t-3)et<0,当
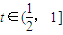 时,S2′=2et+(2t-3)et>0,
时,S2′=2et+(2t-3)et>0,∴t=
 时,S2min=e-2
时,S2min=e-2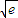 +1.
+1.∴当t变化时,求蜘蛛捕捉住一只苍蝇概率的最小值
p=
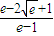 =
= .
.(2)由题设知ξ~B(4,
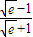 ),
),∴ξ的分布列是P(ξ=k)=
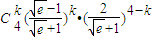 ,k=0,1,2,3,4.
,k=0,1,2,3,4.Eξ=
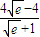 .
.点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,注意定积分的灵活运用.计算量大且繁琐,容易出错,要注意培养计算能力.

练习册系列答案
相关题目
 已知:一窗户满足
已知:一窗户满足