题目内容
(本小题满分12分)
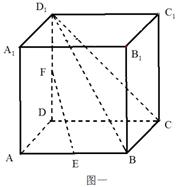
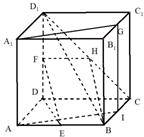
如图一所示,边长为1的正方体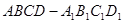 中,
中, 分别为
分别为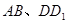 的中点。
的中点。
(Ⅰ)证明: ;
;
(Ⅱ)若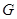 为
为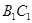 的中点,证明:
的中点,证明: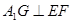 ;
;
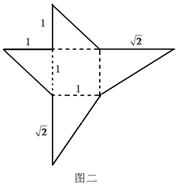
(Ⅲ)如图二所示为一几何体的展开图,沿着图中虚线将它们折叠起来,所得几何体的体积为 ,若正方体
,若正方体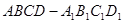 的体积为
的体积为 ,求
,求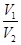 的值。
的值。
【答案】
(Ⅰ)证明:见解析;(Ⅱ)证明:见解析;(Ⅲ)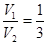 .
.
【解析】本试题主要是考查了空间中点线面的位置关系的综合运用,求解线面平行和线线垂直的问题,以及体积的运算的综合运用。
(1)取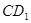 的中点
的中点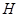 ,连接
,连接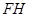 ,
,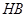 ,然后借助于平行四边形得到线线平行,从而证明线面平行。
,然后借助于平行四边形得到线线平行,从而证明线面平行。
(2)要证明线线垂直,关键是证明线面垂直,然后运用线面垂直的性质定理得到线线垂直的证明。
(3),该几何体为有一条侧棱垂直于底面且底面为正方形的四棱锥,即四棱锥的高为1,底面是边长为1的正方形,因此可以利用整体间的关系的得到比值。
(Ⅰ)证明:取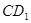 的中点
的中点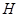 ,连接
,连接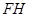 ,
,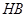 ,
,
∵F、H分别是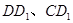 的中点,
的中点,
∴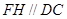 且
且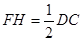 ,
,
∵在正方体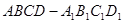 中,
中,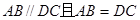 ,
,
又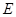 分别为
分别为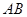 的中点,
的中点,
∴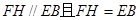 ,
,
∴四边形FHBE为平行四边形,
∴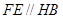 ,
,
又∵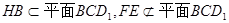 ,
,
∴ ;………………………………………………………………………4分
;………………………………………………………………………4分
(Ⅱ)证明:取BC中点I,连接GI,AI,
在正方形ABCD中,E,I分别为AB,BC的中点,
∴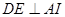 ,
,
∵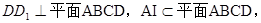
∴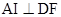 ,
,
又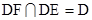 ,
,
∴ ,又
,又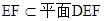 ,
,
∴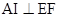
由四边形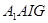 为平行四边形得
为平行四边形得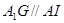 ,
,
∴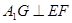 ;……………………………………………………………………………8分
;……………………………………………………………………………8分
(Ⅲ)如图二所示,该几何体为有一条侧棱垂直于底面且底面为正方形的四棱锥,即四棱锥的高为1,底面是边长为1的正方形,
∴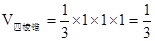 ,又
,又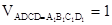 ,
,
∴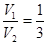 .…………………………………………………………………………………12分
.…………………………………………………………………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目