题目内容
已知函数f(x)=a(2cos2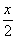 +sinx)+b,
+sinx)+b,
(1)当a=1时,求函数f(x)的单调递增区间;
(2)当a<0,且x∈[0,π]时,函数f(x)的值域为[3,4],求a,b的值。
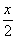 +sinx)+b,
+sinx)+b, (1)当a=1时,求函数f(x)的单调递增区间;
(2)当a<0,且x∈[0,π]时,函数f(x)的值域为[3,4],求a,b的值。
解:(1)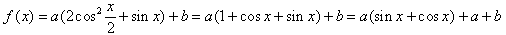
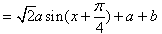 ,
,
若a=1,则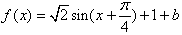 ,
,
由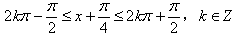 ,
,
得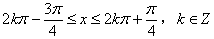 ,
,
∴a=1时,f(x)的单调递增区间为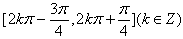 ;
;
(2)由 ,
,
∴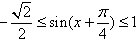 ,
,
又a<0,
∴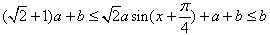 ,
,
依题意,得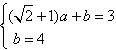 ,
,
解得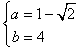 ,
,
故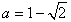 ,b=4。
,b=4。
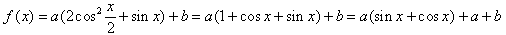
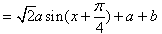 ,
,若a=1,则
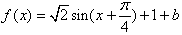 ,
,由
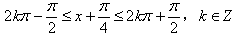 ,
,得
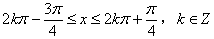 ,
,∴a=1时,f(x)的单调递增区间为
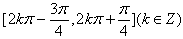 ;
;(2)由
 ,
,∴
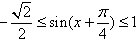 ,
,又a<0,
∴
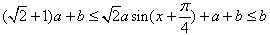 ,
,依题意,得
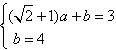 ,
, 解得
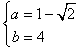 ,
, 故
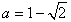 ,b=4。
,b=4。 
练习册系列答案
相关题目