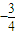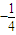题目内容
设函数 ,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是 .
,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是 .
【答案】分析:先设x∈(0,2],则-x∈[-2,0),由奇函数的关系式和题意求出g(x),再由它的解析式和指数、对数函数的单调性判断出g(x)的单调性,进而求出最大值.
解答:解:设x∈(0,2],则-x∈[-2,0),∴f(-x)=2-x= ,
,
∵f(x)是奇函数,∴f(x)=-f(-x)=- =g(x)-
=g(x)- ,
,
得g(x)= -
- ,x∈(0,2],
,x∈(0,2],
∵y= 和y=
和y= 分别是(0,2]上的减函数,增函数,
分别是(0,2]上的减函数,增函数,
∴g(x)= -
- 是(0,2]上的增函数,
是(0,2]上的增函数,
∴当x=2时,g(x)取最大值g(2)= ,
,
故答案为: .
.
点评:本题考查了函数奇偶性的应用,以及复合函数的单调性,根据奇偶性对应的关系式,将所求的函数进行转化,转化到已知范围内求解,考察了转化思想.
解答:解:设x∈(0,2],则-x∈[-2,0),∴f(-x)=2-x=
 ,
,∵f(x)是奇函数,∴f(x)=-f(-x)=-
 =g(x)-
=g(x)- ,
,得g(x)=
 -
- ,x∈(0,2],
,x∈(0,2],∵y=
 和y=
和y= 分别是(0,2]上的减函数,增函数,
分别是(0,2]上的减函数,增函数,∴g(x)=
 -
- 是(0,2]上的增函数,
是(0,2]上的增函数,∴当x=2时,g(x)取最大值g(2)=
 ,
,故答案为:
 .
.点评:本题考查了函数奇偶性的应用,以及复合函数的单调性,根据奇偶性对应的关系式,将所求的函数进行转化,转化到已知范围内求解,考察了转化思想.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 ,若f(x)是奇函数,则
,若f(x)是奇函数,则 的值为
的值为 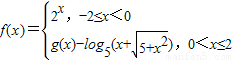 ,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
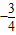

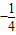
 ,若f(x)是奇函数,则
,若f(x)是奇函数,则 的值为
的值为  ,若f(x)是奇函数,则
,若f(x)是奇函数,则 的值为
的值为 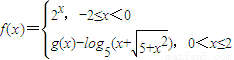 ,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )