题目内容
【题目】设![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和, ![]() .
.
(1)求证:数列![]() 是等差数列,并求
是等差数列,并求![]() 的通项;
的通项;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)证明见解析, 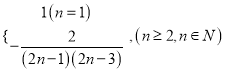 ;(2)
;(2)![]() .
.
【解析】试题分析:当数列提供![]() 与
与![]() 、
、![]() 之间的递推关系时,要数列
之间的递推关系时,要数列![]() 是等差数列,只需利用
是等差数列,只需利用![]() ,转化为
,转化为![]() 、
、![]() 之间的关系,证明某数列是等差数列,就是证明第n+1项与第n项的比是一个常数,这个分析给证明提供一个暗示,有了证明的目标,从递推关系式向着这个目标进行等价变形,就可得出所要证明的式子,达到证明的目的;已知数列的前n项和
之间的关系,证明某数列是等差数列,就是证明第n+1项与第n项的比是一个常数,这个分析给证明提供一个暗示,有了证明的目标,从递推关系式向着这个目标进行等价变形,就可得出所要证明的式子,达到证明的目的;已知数列的前n项和![]() ,求通项公式分两步,第一步n=1 时,求出首项,第二步,当
,求通项公式分两步,第一步n=1 时,求出首项,第二步,当![]() 时利用前n项和与前n-1项和作差求出第n项,若首项满足后者,则可书写统一的通项公式,若首项不满足,则通项公式要写成分段函数形式,有关数列求和问题,主要方法有倒序相加法、错位相减法、分组求和法、公式法等,要根据数列通项的形式特点采用相应的方法求和.
时利用前n项和与前n-1项和作差求出第n项,若首项满足后者,则可书写统一的通项公式,若首项不满足,则通项公式要写成分段函数形式,有关数列求和问题,主要方法有倒序相加法、错位相减法、分组求和法、公式法等,要根据数列通项的形式特点采用相应的方法求和.
试题解析:
(1)![]()
![]() ,∴
,∴![]() ,
,
即![]() ,
, ![]() ,
,
∴数列![]() 是等差数列.
是等差数列.
由上知数列![]() 是以2为公差的等差数列,首项为
是以2为公差的等差数列,首项为![]() ,
,
∴![]() ,∴
,∴![]() .
.
∴![]() .
.
(或由![]() 得
得![]() ),
),
由题知, ![]() ,
,
综上, 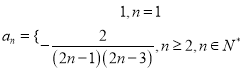 .
.
(2)由(1)知![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目