题目内容
如图,在长方体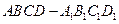 中,
中,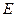 、
、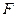 分别是棱
分别是棱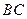 ,
,
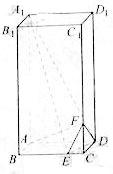
上的点, ,
,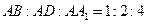
(1) 求异面直线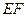 与
与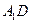 所成角的余弦值;
所成角的余弦值;
(2) 证明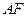
 平面
平面
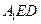
(3) 求二面角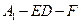 的正弦值。
的正弦值。
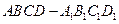 中,
中,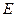 、
、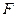 分别是棱
分别是棱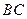 ,
,

上的点,
 ,
,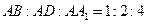
(1) 求异面直线
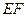 与
与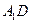 所成角的余弦值;
所成角的余弦值;(2) 证明
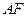
 平面
平面
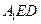
(3) 求二面角
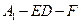 的正弦值。
的正弦值。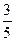 ,
,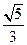
方法一:如图所示,建立空间直角坐标系,
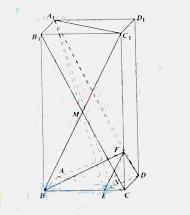
点A为坐标原点,设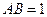 ,依题意得
,依题意得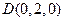 ,
,
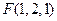 ,
,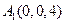 ,
,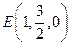
(1) 解:易得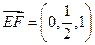 ,
,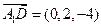
于是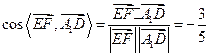
所以异面直线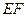 与
与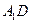 所成角的余弦值为
所成角的余弦值为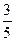
(2) 证明:已知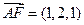 ,
,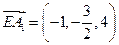 ,
,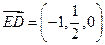
于是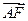 ·
·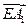 =0,
=0,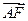 ·
·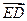 =0.因此,
=0.因此,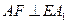 ,
,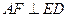 ,又
,又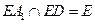
所以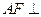 平面
平面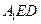
(3)解:设平面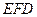 的法向量
的法向量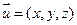 ,则
,则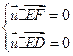 ,即
,即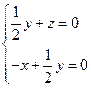
不妨令X=1,可得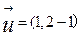 。由(2)可知,
。由(2)可知,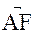 为平面
为平面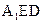 的一个法向量。
的一个法向量。
于是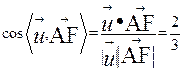 ,从而
,从而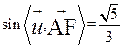
所以二面角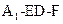 的正弦值为
的正弦值为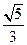
方法二:(1)解:设AB=1,可得AD=2,AA1=4,CF=1.CE=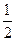
链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由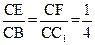 ,可知EF∥BC1.故
,可知EF∥BC1.故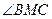 是异面直线EF与A1D所成的角,易知BM=CM=
是异面直线EF与A1D所成的角,易知BM=CM=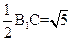 ,所以
,所以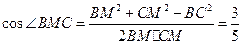 ,所以异面直线FE与A1D所成角的余弦值为
,所以异面直线FE与A1D所成角的余弦值为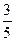
(2)证明:连接AC,设AC与DE交点N 因为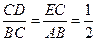 ,所以
,所以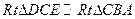 ,从而
,从而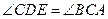 ,又由于
,又由于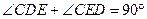 ,所以
,所以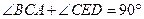 ,故AC⊥DE,又因为CC1⊥DE且
,故AC⊥DE,又因为CC1⊥DE且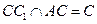 ,所以DE⊥平面ACF,从而AF⊥DE.
,所以DE⊥平面ACF,从而AF⊥DE.
连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D因为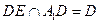 ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:连接A1N.FN,由(2)可知DE⊥平面ACF,又NF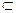 平面ACF, A1N
平面ACF, A1N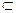 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故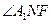 为二面角A1-ED-F的平面角
为二面角A1-ED-F的平面角
易知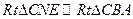 ,所以
,所以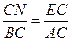 ,又
,又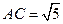 所以
所以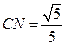 ,在
,在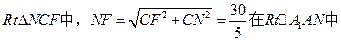

连接A1C1,A1F 在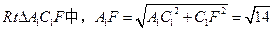
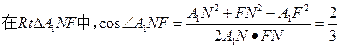 。所以
。所以
所以二面角A1-DE-F正弦值为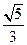

点A为坐标原点,设
 ,依题意得
,依题意得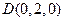 ,
,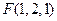 ,
,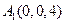 ,
,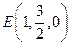
(1) 解:易得
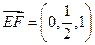 ,
,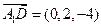
于是
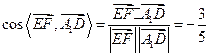
所以异面直线
 与
与 所成角的余弦值为
所成角的余弦值为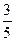
(2) 证明:已知
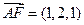 ,
,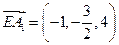 ,
,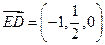
于是
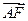 ·
·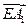 =0,
=0,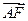 ·
·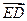 =0.因此,
=0.因此,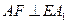 ,
,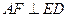 ,又
,又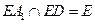
所以
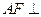 平面
平面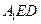
(3)解:设平面
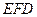 的法向量
的法向量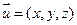 ,则
,则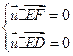 ,即
,即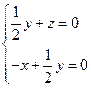
不妨令X=1,可得
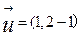 。由(2)可知,
。由(2)可知,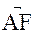 为平面
为平面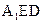 的一个法向量。
的一个法向量。于是
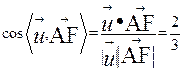 ,从而
,从而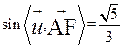
所以二面角
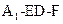 的正弦值为
的正弦值为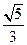
方法二:(1)解:设AB=1,可得AD=2,AA1=4,CF=1.CE=
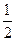
链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由
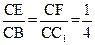 ,可知EF∥BC1.故
,可知EF∥BC1.故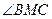 是异面直线EF与A1D所成的角,易知BM=CM=
是异面直线EF与A1D所成的角,易知BM=CM=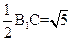 ,所以
,所以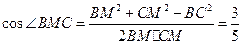 ,所以异面直线FE与A1D所成角的余弦值为
,所以异面直线FE与A1D所成角的余弦值为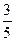
(2)证明:连接AC,设AC与DE交点N 因为
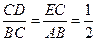 ,所以
,所以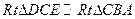 ,从而
,从而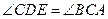 ,又由于
,又由于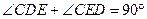 ,所以
,所以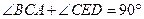 ,故AC⊥DE,又因为CC1⊥DE且
,故AC⊥DE,又因为CC1⊥DE且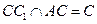 ,所以DE⊥平面ACF,从而AF⊥DE.
,所以DE⊥平面ACF,从而AF⊥DE.连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D因为
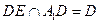 ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED(3)解:连接A1N.FN,由(2)可知DE⊥平面ACF,又NF
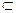 平面ACF, A1N
平面ACF, A1N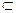 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故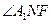 为二面角A1-ED-F的平面角
为二面角A1-ED-F的平面角易知
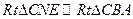 ,所以
,所以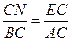 ,又
,又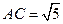 所以
所以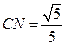 ,在
,在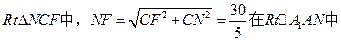

连接A1C1,A1F 在
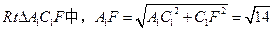
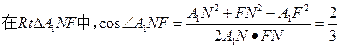 。所以
。所以
所以二面角A1-DE-F正弦值为
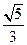

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
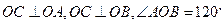 , 且
, 且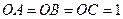
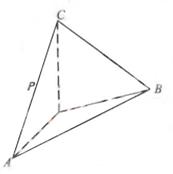
 为
为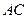 的中点,证明:在
的中点,证明:在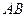 上存在一点
上存在一点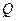 ,使
,使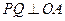 ,并计算
,并计算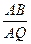 的值;
的值;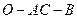 的平面角的余弦值。
的平面角的余弦值。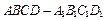 中,点
中,点 在棱
在棱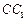 的延长线上,且
的延长线上,且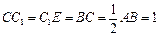 .下标
.下标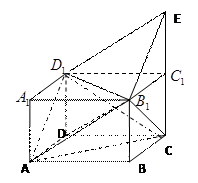
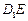 ∥平面
∥平面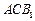 ;
;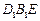
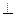 平面
平面 ;
;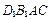 的体积.
的体积.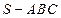 中,底面
中,底面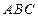 为边长等于2的等边三角形,
为边长等于2的等边三角形,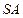 垂直于底面
垂直于底面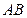 与平面
与平面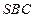 所成角的正弦值为
所成角的正弦值为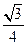
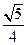
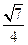
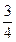
 E是棱
E是棱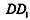 的中点。
的中点。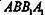 所成的角的正弦值;
所成的角的正弦值;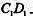 上是否存在一点F,使
上是否存在一点F,使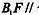 平面
平面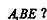 证明你的结论。
证明你的结论。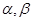 是不同的两个平面,直线
是不同的两个平面,直线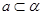 ,直线
,直线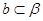 ,条件
,条件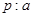 与
与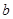 没有公共点,条件
没有公共点,条件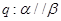 ,则
,则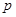 是
是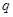 的
的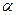 、
、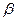 是两个不同平面,
是两个不同平面,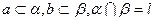 ,则( )
,则( )